学过矩阵理论或者线性代数的肯定知道正交矩阵(orthogonal matrix)是一个非常好的矩阵,为什么这么说?原因有一下几点:
以上可以看出正交矩阵是非常特殊的矩阵,而本文题目中的旋转矩阵就是一种正交矩阵!它完美的诠释了正交矩阵的所有特点。
先说一下什么是旋转矩阵?如图1所示,我们假设最开始空间的坐标系XA,YA,Z就是笛卡尔坐标系,这样我们得到空间A的矩阵VA={XA,YA,ZA}T,其实也可以看做是单位阵E。进过旋转后,空间A的三个坐标系变成了图1中红色的三个坐标系XB,YB,ZB,得到空间B的矩阵VB={XB,YB,ZB}T。我们将两个空间联系起来可以得到VB=R•VA,这里R就是我们所说的旋转矩阵。由于XA={1,0,0}T,YA={0,1,0}T,ZA={0,0,1}T,结合图2可以看出,旋转矩阵R就是由XB,YB,ZB 三个向量组成的。讲到这里,大家应该会发现旋转矩阵R满足第一个条件,因为单位向量无论怎么旋转长度肯定不会变而且向量之间的正交性质也不会变。那么旋转矩阵就是正交阵!不过这还不能说明问题,下面我更进一步利用数学公式进行证明。
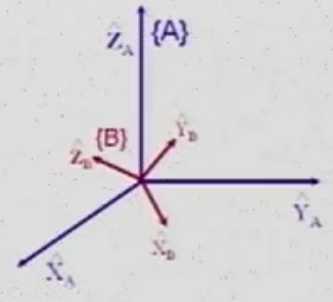
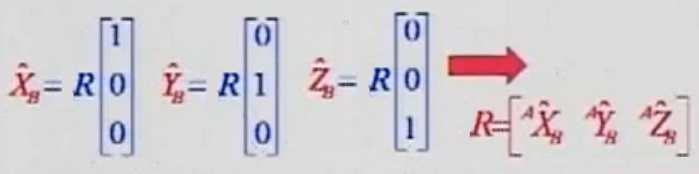
图1 图2
说一般的情况前,我们先说两点数学知识。(1)点乘(dot product)的几何意义:如图3,我们从点乘的公式可以得到α•β相当与β的模乘上α在β上投影的模,所以当|β|=1时,α•β就是指α在β上投影的模。这一点在下面的内容中非常重要。(2)旋转矩阵逆的几何意思:这个比较抽象,不过也好理解。旋转矩阵相当于把一个向量(空间)旋转成新的向量(空间),那么逆可以理解为由新的向量(空间)转回原来的向量(空间)。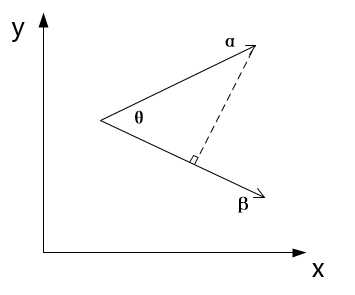
图3
接下来就是重点了,我们结合图4进行分析。上面已经说明了,旋转矩阵R就是由XB,YB,ZB 三个向量组成的。我们来看看XB,YB,ZB究竟是什么?由于图中所有的向量均是单位向量,所以XB与XA点乘的结果可以看成XB在XA上的投影的模,也就是XB在空间A中x轴的分量!!图中中间的位置列出了XB向量中的三个分量分别为XB在XA上的投影的模、XB在YA上的投影的模和XB在ZA上的投影的模。这从几何角度很好理解。以此类推,可以得出的旋转矩阵R的表达形式。我们根据图4可以惊喜的发现,矩阵R的第一行就是XA在XB,YB,ZB上的投影的模,也就是XAT。这个发现有什么用呢?图5做出解释。根据上面公式可以推出A到B的旋转矩阵等于B到A的旋转矩阵的转置。根据我们上一段所说的A到B的旋转矩阵的逆就是等于B到A的旋转矩阵,因此很容易推出R-1等于RT!这满足正交矩阵的第二个条件,又一次证明了旋转矩阵就是正交阵。在平时的工作中,我也测试过所有的旋转矩阵的行列式的值都是为1的,所以旋转矩阵满足正交阵的一切性质,可以说是很完美的矩阵。
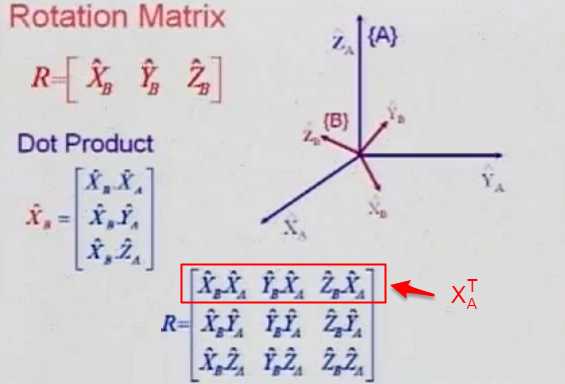

图4 图5
明天举一些列子来说明旋转矩阵的性质,先到这。
原文:http://www.cnblogs.com/caster99/p/4703033.html