贪心的思路很明显,每次选择点权最小的走,一边走一边记录路径,
很容易想到如果出现环,那么之后没有记录到路径的点就不可能到达了,因为它会不断绕环走
于是想到记录点有没有被访问,但是这样做就掉坑里了,如下图
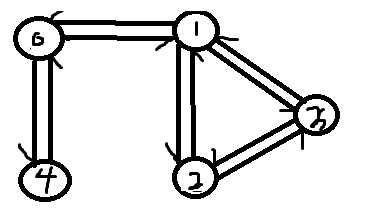
起点是0
那么4 的路径就是0->1->2->3->1->0->4
所以我们得换个思路,记录有向边有没有被访问
如果被访问,说明存在环,剩下的点都不可达
但是这样还存在问题,就是要避免走到没有环的一支,
于是开个数组记录点被访问了多少次,2次以上的,说明存在环,是可以走回来的

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <vector> 5 #define pb push_back 6 using namespace std; 7 int t,n,m,s; 8 bool e[110][110],ok; 9 int vis[110][110],check[110]; 10 vector<int> ans[110],tmp[110]; 11 void init(){ 12 ok=0; 13 memset(check,0,sizeof check); 14 memset(e,0,sizeof e); 15 memset(vis,0,sizeof vis); 16 for(int i=0;i<110;i++) ans[i].clear(),tmp[i].clear(); 17 } 18 void read(){ 19 scanf("%d%d%d",&n,&m,&s); 20 init(); 21 int u,v; 22 for(int i=0;i<m;i++){ 23 scanf("%d%d",&u,&v); 24 e[u][v]=e[v][u]=1; 25 } 26 } 27 void dfs(int x,int fa){ 28 for(int i=0;i<n;i++){ 29 if(i==fa) continue; 30 if(e[x][i]){ 31 //cout<<x<<"->"<<i<<endl; 32 if(vis[x][i]&&check[i]>=2) {ok=1;return;} 33 if(!check[i]){ 34 ans[i]=tmp[x],ans[i].pb(i); 35 } 36 check[i]++; 37 tmp[i]=tmp[x],tmp[i].pb(i); 38 vis[x][i]=1; 39 dfs(i,x); 40 if(ok) return; 41 } 42 } 43 } 44 void solve(int ca){ 45 check[s]=1; 46 ans[s].pb(s); 47 tmp[s].pb(s); 48 dfs(s,-1); 49 printf("Case #%d:\n",ca); 50 for(int i=0;i<n;i++){ 51 if(ans[i].size()==0) printf("No drive.\n"); 52 else{ 53 int z=ans[i].size(); 54 printf("%d",ans[i][0]); 55 for(int j=1;j<z;j++) printf(" %d",ans[i][j]); 56 printf("\n"); 57 } 58 } 59 printf("\n"); 60 } 61 int main(){ 62 scanf("%d",&t); 63 for(int ca=1;ca<=t;ca++){ 64 read(); 65 solve(ca); 66 } 67 return 0; 68 }
uva10802 Lex Smallest Drive(贪心+dfs),布布扣,bubuko.com
uva10802 Lex Smallest Drive(贪心+dfs)
原文:http://www.cnblogs.com/wonderzy/p/3628809.html