很高端的理论,一下来自维基百科。
在图论中,标号树的普吕弗(Prüfer)序列是由树唯一地产生的序列。n顶点的标号树有长n ? 2的普吕弗序列,可以从一个简单的迭代算法得到。普吕弗序列在1918年首先由海因茨·普吕弗用来证明凯莱公式。
一棵树要得到普吕弗序列,方法是逐次去掉树的顶点,直到剩下两个顶点。考虑树T,其顶点为{1, 2, ..., n}。在第i步,去掉标号最小的叶,并把普吕弗序列的第i项设为这叶的邻顶点的标号。
一棵树的序列明显是唯一的,而且长为n ? 2。
把上述算法用在右图标号树。第一步,顶点1是最小标号的叶,因此首先去掉,普吕弗序列首项是"4",接着去掉顶点2和3,"4"两次加进序列。顶点4现在是叶,去掉后剩下2个顶点,所以把"5"加进序列后结束。树的序列是{4,4,4,5}。
从一个普吕弗序列,可以求得一棵树有这一普吕弗序列。
设这普吕弗序列长n ? 2。首先写出数1至n。第一步,找出1至n中没有在序列中出现的最小数。把标号为这数的顶点和标号为序列首项的顶点连起来,并把这数从1至n中删去,序列的首项也删去。接着每一步以1至n中剩下的数和余下序列重复以上步骤。最后当序列用完,把1至n中最后剩下的两数的顶点连起来。
一棵树的序列明显地是唯一的,但比较不明显的是,一个长为n?2且每项都在1至n之间的序列S,有唯一的标号树以S为普吕弗序列。这个结果可以对n用数学归纳法证明。
从这结果立刻可知,普吕弗序列给出长n?2的序列和有n顶点的标号树之间的一一映射。长n?2的序列共有nn?2个,这样就证明了凯莱公式,就是n顶点的标号树共有nn?2棵。
这个结果可以推广:一棵标号树实际上是标号完全图的一棵生成树。对普吕弗序列加以限制。类似的方法可以得到标号完全二部图的生成树总数。若G是完全二部图,一部分的顶点标号1到n1,另一部分的顶点标号n1 + 1到n。G的标号生成树总数为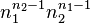 ,其中n2 = n ? n1。
,其中n2 = n ? n1。
原文:http://www.cnblogs.com/acvc/p/3629227.html