题目是这样的:A B两地距离1000km,A地有3000吨煤。A地有一辆火车,单次最大运载量为1000吨,每行驶 1km要消耗
1吨煤。现在要把这3000吨煤从A运输到B,求运到B最多还有多少吨煤?
对于这个问题,我想到了创建一个模型,根据题目要求得出初始状态、终极状态和中间条件,这里用一张图表示。
初始状态:A=3000, x = y = 0, B = 0
结束状态:A= 0, y - x = 1000, B + x + y = 3000
这里 火车单次最大负载 maxLoad = 1000, 煤总量 为 3000, 因此将路程 3000/1000 = 3
比较合适(这里不做证明)
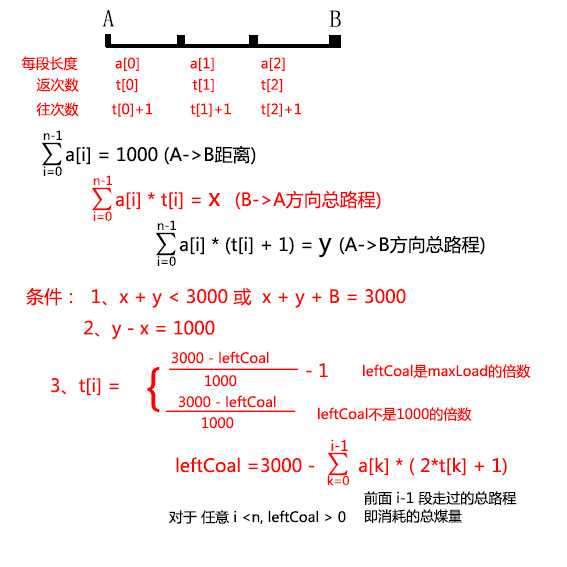
看图分析可得,对于每段路程,往次数总是比返次数多1 ,所以可以推出
a[0] + a[1] + a[2] = 1000
所有条件均已在途中列出。 如果不能理解上图,可以考虑一种实际情况 a[0] = a[1] = 250, a[2] = 500。
下一个问题,就是如何通过编程来找出B的最大值。由于 a[0] + a[1] + a[2] = 1000,因此,可以用遍历的方法实现。
代码如下
#include <stdio.h>
#include <stdlib.h>
int main(){
FILE *
out;
int total =
3000;
int a[] = {
1,
1,
1};
// 记录每段 长度, 总长度为 1000 km
int t[] = {
0,
0,
0};
// 记录每段路 返回经过的次数
int x =
0, xb =
0;
int xy =
0, xyb =
0;
// x + y
int remain, remainb;
int i, j;
int max =
0;
// 创建一个文件,用来记录结果
if((
out=fopen(
"res.txt",
"a++"))==NULL){
fprintf(stdout,
"Cannot open \"res.txt\" file\n");
exit(
1);
}
// invariant: a[0] + a[1] + a[2] = 1000
// invariant: 剩下的煤量超过剩下的距离
for(i =
1; i <
500; i++){
a[
0] = i;
// 第一段路程 0001
t[
0] =
2;
xb = a[
0] * t[
0];
xyb = a[
0] * (
2 * t[
0] +
1);
remainb = total - xyb;
// 记录 x, xy, remain 以便于在内层循环起始处恢复
for(j =
1; j <
500; j++){
x = xb, xy = xyb, remain = remainb;
// 每次都重新对 x, xy, remain赋值
a[
1] = j;
// 第二段路程 0002
t[
1] = remain %
1000 ==
0? (remain/
1000 -
1):(remain/
1000);
x += a[
1] * t[
1];
xy += a[
1] * (
2 * t[
1] +
1);
if(x>=
1000)
continue;
// x + y < 3000, 所以2 * x < 2000, 即 x < 1000
if(xy>=
3000)
continue;
// x + y < 3000
remain = total - xy;
a[
2] =
1000 - i - j;
// 第三段路程 0003
if(a[
2] > remain)
continue;
t[
2] = remain %
1000 ==
0? (remain/
1000 -
1):(remain/
1000);
x += a[
2] * t[
2];
xy += a[
2] * (
2 * t[
2] +
1);
if(x>=
1000)
continue;
// x + y < 3000, 所以2 * x < 2000, 即 x < 1000
if(xy>=
3000)
continue;
// x + y < 3000
remain = total - xy;
// 将 结果打印到 文件中,便于查看
fprintf(
out,
"i = %d, j = %d, x = %d, xy = %d, r = %d\n", i, j, x, xy, r);
if(remain > max) max = remain;
}
// end of innner for loop j
}
// end of outer for (i
printf(
"max = %d\n", max);
if(fclose(
out)!=
0){
fprintf(stdout,
"close failed");
}
getchar();
return 0;
}
之所以去 a[0] , a[1] 范围 是 1-500, 是因为除最后一段路不需要返回以外,其它都需要。需要返回,同时最大载货量为
1000,所以前进距离最多为 500。否则火车就白跑了。
如果 煤的总量扩展到 3000 * N, 使用循环不靠谱了,不过应该可以用回溯法来实现。
这种方法的另一个漏洞是,只能遍历整数,而数学上的最优解,是一个小数。这一点我还无法克服。
火车运煤问题(驴运萝卜问题),布布扣,bubuko.com
火车运煤问题(驴运萝卜问题)
原文:http://www.cnblogs.com/oscarzhao/p/3629804.html
