统计中的t检验

1.什么情况下，应用t检验

2. 我们的目的，就是要检验这个总体均值m是否合理　　

3.具体步骤：

参考：http://wiki.mbalib.com/wiki/T%E6%A3%80%E9%AA%8C

T检验的步骤

　　1、建立虚无假设H₀:μ₁ = μ₂，即先假定两个总体平均数之间没有显著差异；

　　2、计算统计量t值，对于不同类型的问题选用不同的统计量计算方法；

　　1）如果要评断一个总体中的小样本平均数与总体平均值之间的差异程度，其统计量t值的计算公式为：

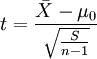
　　2）如果要评断两组样本平均数之间的差异程度，其统计量t值的计算公式为：

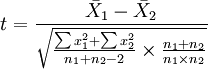
　　3、根据自由度df=n-1，查t值表，找出规定的t理论值并进行比较。理论值差异的显著水平为0.01级或0.05级。不同自由度的显著水平理论值记为t(df)0.01和t(df)0.05

　　4、比较计算得到的t值和理论t值，推断发生的概率，依据下表给出的t值与差异显著性关系表作出判断。

T值与差异显著性关系表
t	P值	差异显著程度
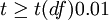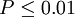		差异非常显著
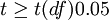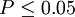		差异显著
t < t(df)0.05	P > 0.05	差异不显著

　　5、根据是以上分析，结合具体情况，作出结论。

————————————————————————————————————————————————————————

统计量是随机变量的函数

常规的概率分布是考查随机变量的取值的可能性。

统计量是在此基础上做推广，对随机变量进行组合，得到统计量。根据既有的假设，我们会考虑统计量是服从某种特定的分布。

在统计量的这个模型下，考查统计值的分布，哪些是统计值：样本均值、样本方差，样本个数。

最终，可以在 A：统计量所服从的分布模型 +B：我们所现有的一个样本（得到样本均值、样本方差，样本个数），然后做推断 C：这个样本 B 在这个 假设 A下是否合理。

统计中的t检验,布布扣,bubuko.com

统计中的t检验

原文：http://www.cnblogs.com/haore147/p/3630154.html