Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2247 Accepted Submission(s): 940
题目大意:
N个点,每个点都有各自的cost, 然后M 无向条边
要求割去S点到D路线中的点,使之无法从S到D ,而且要求消耗的cost和最小.
这是一道网络流的题. 算的是最小割. 根据最大流最小割定理. 可以直接算最大流;
但是这题的的流量限制是在点上的.所以要我们来拆点.
我这题是把i 点的 点首和点尾 分别设为 i 和 i+n; 显然 最后会得到2*n个点
如图:
将点1拆分成两部分分别为点首1和点尾1+n,然后把点首到点尾的流量限制设成 题目要求的cost; ,点1---->(1+n)的花费即为封锁城市1的代价
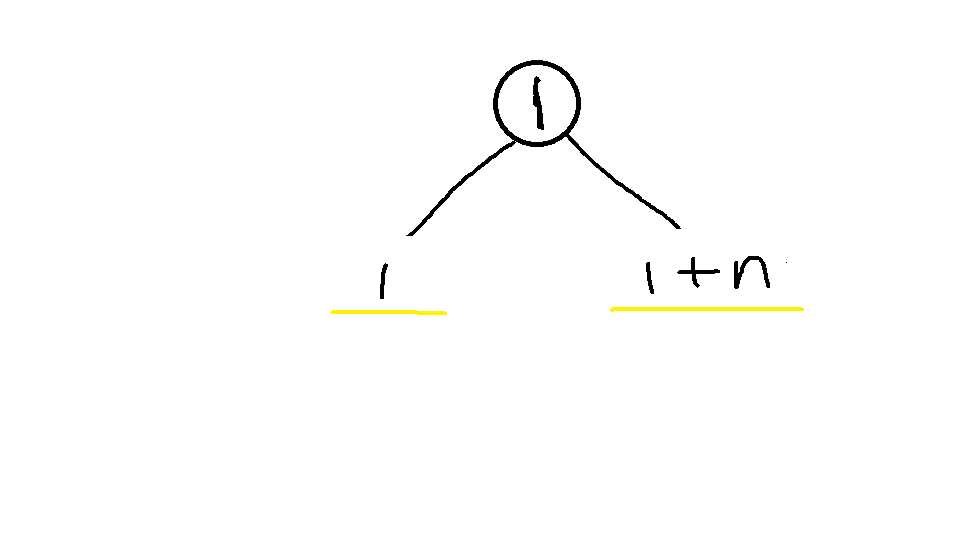
而点与点之间(两座城市之间)的边,要设成正无穷大, 因为边不消耗cost;
然后从S的点首S 跑到 D的点尾 D+n 就可以计算出最小割了.

#include<stdio.h> #include<algorithm> #include<queue> #include<string.h> #define N 510 #define INF 0x3f3f3f3f using namespace std; struct Edge { int u, v, flow, next; } edge[N * N]; int layer[N], head[N], cnt; void Init() { memset(head, -1, sizeof(head)); cnt = 0; } void AddEdge(int u, int v, int flow) { edge[cnt].u = u; edge[cnt].v = v; edge[cnt].flow = flow; edge[cnt].next = head[u]; head[u] = cnt++; swap(u, v); edge[cnt].u = u; edge[cnt].v = v; edge[cnt].flow = 0; edge[cnt].next = head[u]; head[u] = cnt++; } bool BFS(int Start, int End) { queue<int>Q; memset(layer, -1, sizeof(layer)); Q.push(Start); layer[Start] = 1; while(!Q.empty()) { int u = Q.front(); Q.pop(); if(u == End) return true; for(int i = head[u] ; i != -1 ; i = edge[i].next) { int v = edge[i].v; if(layer[v] == -1 && edge[i].flow > 0) { layer[v] = layer[u] + 1; Q.push(v); } } } return false; } int DFS(int u, int Maxflow, int End) { if(u == End) return Maxflow; int uflow = 0; for(int i = head[u] ; i != -1 ; i = edge[i].next) { int v = edge[i].v; if(layer[v] == layer[u] + 1 && edge[i].flow > 0) { int flow = min(edge[i].flow, Maxflow - uflow); flow = DFS(v, flow, End); edge[i].flow -= flow; edge[i^1].flow += flow; uflow += flow; if(uflow == Maxflow) break; } } if(uflow == 0) layer[u] = 0; return uflow; } int Dinic(int Start, int End) { int Maxflow = 0; while(BFS(Start, End)) Maxflow += DFS(Start, INF, End); return Maxflow; } int main() { int m, n, s, t; while(~scanf("%d%d", &m, &n)) { Init(); scanf("%d%d", &s, &t); int u, v, flow; for(int i = 1 ; i <= m ; i++) { scanf("%d", &flow); AddEdge(i, i + m, flow); } while(n--) { scanf("%d%d", &u, &v); AddEdge(u + m, v, INF); AddEdge(v + m, u, INF); } printf("%d\n", Dinic(s, t + m)); } return 0; }
原文:http://www.cnblogs.com/qq2424260747/p/4729312.html