本文共可分为如下几个部分组成:
地球椭球体(Ellipsoid)
大地基准面(Geodetic datum)
投影坐标系统(Projected Coordinate Systems )
坐标系统和投影变换在桌面产品中的应用
GIS处 理的是空间信息,而所有对空间信息的量算都是基于某个坐标系统的,因此GIS中坐标系统的定义是GIS系统的基础,正确理解GIS中的坐标系统就变得尤为 重要。坐标系统又可分为两大类:地理坐标系统、投影坐标系统。本文就对坐标系和投影及其在ArcGIS桌面产品中的应用做一些简单的论述。
GIS中的坐标系定义由基准面和地图投影两组参数确定,而基准面的定义则由特定椭球体及其对应的转换参数确定,因此欲正确定义GIS系统坐标系,首先必须弄清地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念及它们之间的关系。
众所周知我们的地球表面是一个凸凹不平的表面,而对 于地球测量而言,地表是一个无法用数学公式表达的曲面,这样的曲面不能作为测量和制图的基准面。假想一个扁率极小的椭圆,绕大地球体短轴旋转所形成的规则 椭球体称之为地球椭球体。地球椭球体表面是一个规则的数学表面,可以用数学公式表达,所以在测量和制图中就用它替代地球的自然表面。因此就有了地球椭球体的概念。
地球椭球体有长半径和短半径之分,长半径(a)即赤道半径,短半径(b)即极半径。f=(a-b)/a为椭球体的扁率,表示椭球体的扁平程度。由此可见,地球椭球体的形状和大小取决于a、b、f 。因此,a、b、f被称为地球椭球体的三要素。
ArcGIS(ArcInfo)桌面软件中提供了30种地球椭球体模型;常见的地球椭球体数据见下表:
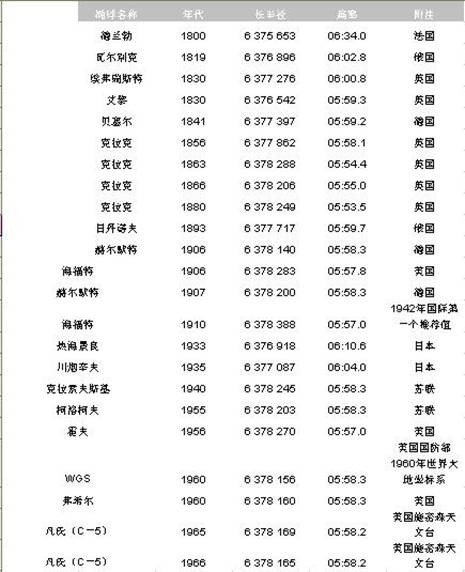
对地球椭球体而言,其围绕旋转的轴叫地轴。地轴的北 端称为地球的北极,南端称为南极;过地心与地轴垂直的平面与椭球面的交线是一个圆,这就是地球的赤道;过英国格林威治天文台旧址和地轴的平面与椭球面的交 线称为本初子午线。以地球的北极、南极、赤道和本初子午线等作为基本要素,即可构成地球椭球面的地理坐标系统(A geographic coordinate system (GCS) uses a threedimensional spherical surface to define locations on the earth.A GCS includes an angular unit of measure, a prime meridian,and a datum (based on a spheroid).)。可以看出地理坐标系统是球面坐标系统,以经度/维度(通常以十进制度或度分秒(DMS)的形式)来表示地面点位的位置。
地理坐标系统以本初子午线为基准(向东,向西各分了1800)之东为东经其值为正,之西为西经其值为负;以赤道为基准(向南、向北各分了900)之北为北纬其值为正,之南为南纬其值为负。
地表任意位置的坐标值可由图2表达:
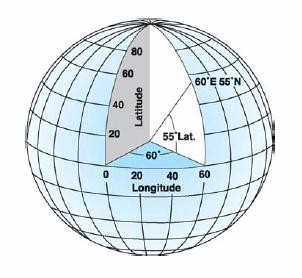
图2地理坐标系统
大地基准面(Geodetic datum),设计用为最密合部份或全部大地水准面的数学模式。它由椭球体本身及椭球体和地表上一点视为原点间之关系来定义。此关系能以 6个量来定义,通常(但非必然)是大地纬度、大地经度、原点高度、原点垂线偏差之两分量及原点至某点的大地方位角。
先抛开测绘学上这个晦涩难懂的概念,看看GIS系统中的基准面是如何定义的,GIS中的基准面通过当地基准面向WGS1984的转换7参数来定义,转换通过相似变换方法实现,具体算法可参考科学出版社1999年出版的《城市地理信息系统标准化指南》第76至86页。假设Xg、Yg、Zg表示WGS84地心坐标系的三坐标轴,Xt、Yt、Zt表示当地坐标系的三坐标轴,那么自定义基准面的7参数分别为:三个平移参数ΔX、ΔY、ΔZ表示两坐标原点的平移值;三个旋转参数εx、εy、εz表示当地坐标系旋转至与地心坐标系平行时,分别绕Xt、Yt、Zt的旋转角;最后是比例校正因子,用于调整椭球大小。
把地球椭球体和基准面结合起来看,如果把地球比做是“马铃薯”,表面凸凹不平,而地球椭球体就好比一个“鸭蛋”,那么按照前面的定义,基准面就定义了怎样拿这个“鸭蛋”去逼近“马铃薯”某一个区域的表面,X、Y、Z轴进行一定的偏移,并各自旋转一定的角度,大小不适当的时候就缩放一下“鸭蛋”,这样通过如上的处理必定可以达到很好的逼近地球某一区域的表面。
因此,每个国家或地区均有各自的基准面,我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系,1978年采用国际大地测量协会推荐的1975地球椭球体(IAG75)建立了我国新的大地坐标系--西安80坐标系,目前大地测量基本上仍以北京54坐标系作为参照,北京54与西安80坐标之间的转换可查阅国家测绘局公布的对照表。 WGS1984基准面采用WGS84椭球体,它是一地心坐标系,即以地心作为椭球体中心,目前GPS测量数据多以WGS1984为基准。
克拉索夫斯基(Krassovsky)、1975地球椭球体(IAG75)、WGS1984椭球体的参数可以参考常见的地球椭球体数据表。
椭球体与基准面之间的关系是一对多的关系,也就是基准面是在椭球体基础上建立的,但椭球体不能代表基准面,同样的椭球体能定义不同的基准面。地球椭球体和基准面之间的关系以及基准面是如何结合地球椭球体从而实现来逼近地球表面的可以通过图3一目了然。
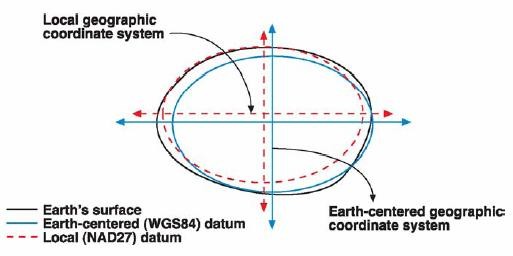
图3 基准面定义椭球体拟合地表某一区域表面
地球椭球体表面也是个曲面,而我们日常生活中的地图及量测空间通常是二维平面,因此在地图制图和线性量测时首先要考虑把曲面转化成平面。由于球面上任何一点的位置是用地理坐标(λ,φ)表示的,而平面上的点的位置是用直角坐标(χ,у)或极坐标(r, )表示的,所以要想将地球表面上的点转移到平面上,必须采用一定的方法来确定地理坐标与平面直角坐标或极坐标之间的关系。这种在球面和平面之间建立点与点之间函数关系的数学方法,就是地图投影方法。
接下来首先让我们来看看ArcGIS产品中对于北京54投影坐标系统的定义参数:
Projection: Gauss_Kruger
Parameters:
False_Easting: 500000.000000
False_Northing: 0.000000
Central_Meridian: 117.000000
Scale_Factor: 1.000000
Latitude_Of_Origin: 0.000000
Linear Unit: Meter (1.000000)
Geographic Coordinate System:
Name: GCS_Beijing_1954
Alias:
Abbreviation:
Remarks:
Angular Unit: Degree (0.017453292519943299)
Prime Meridian: Greenwich (0.000000000000000000)
Datum: D_Beijing_1954
Spheroid: Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000
从参数中可以看出,每一个投影坐标系统都必定会有Geographic Coordinate System(地理坐标系统)。 那么我们从这一角度上解释一下投影和投影所需要的必要条件:将球面坐标转化为平面坐标的过程便是投影过程;投影所需要的必要条件是:第一、任何一种投影都 必须基于一个椭球(地球椭球体),第二、将球面坐标转换为平面坐标的过程(投影算法)。简单的说投影坐标系是地理坐标系+投影过程。
下面从透视法(地图投影方法的一种)角度来直观的理解投影,如图4:
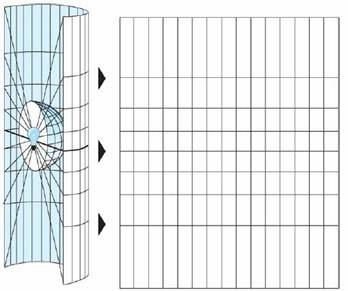
图4 透视法投影示意图
几何透视法是利用透视的关系,将地球体面上的点投影到投影面(借助的几何面)上的一种投影方法。如假设地球按比例缩小成一个透明的地球仪般的球体,在其球心或球面、球外安置一个光源,将球面上的经纬线投影到球外的一个投影平面上。
投影既然是一种数学变换方法,那么任何一种投影都存在一定的变形,因此可以按照变形性质将投影方法如下分类:等角投影(Conformal Projection)、等积投影(Equal Area Projection)、等距投影(Equidistant Projection)、等方位投影(True-direction Projection)四种。每种投影根据其名称就可以知道其方法保证了数据的那些几何属性,在实际应用过程中应根据需求来选取某种投影。
如果按照投影的构成方法分类又可分为方位、圆柱、圆锥投影三种,在上述三种投影中由于几何面与球面的关系位置不同,又分为正轴、横轴和斜轴三种。如图5-7:
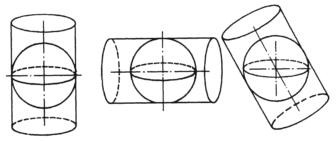
图5 正、横、斜圆柱投影示意图
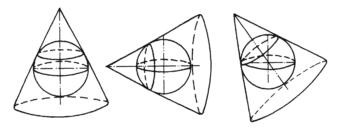
图6 正、横、斜圆锥投影示意图
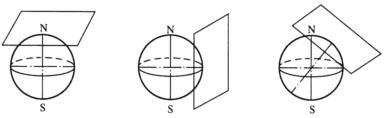
图7 正、横、斜方位投影示意图
我国通常采用的投影——高斯—克吕格(Gauss-Kruger)投影,是一种“等角横切圆柱投影”。德国数学家、物理学家、天文学家高斯(Carl Friedrich Gauss,1777一 1855)于十九世纪二十年代拟定,后经德国大地测量学家克吕格(Johannes Kruger,1857~1928)于 1912年 对投影公式加以补充,故名。设想用一个圆柱横切于球面上投影带的中央经线,按照投影带中央经线投影为直线且长度不变和赤道投影为直线的条件,将中央经线两 侧一定经差范围内的球面正形投影于圆柱面。然后将圆柱面沿过南北极的母线剪开展平,即获高斯-克吕格投影平面。高斯—克吕格投影后,除中央经线和赤道为直 线外,其他经线均为对称于中央经线的曲线。高斯—克吕格投影没有角度变形,在长度和面积上变形也很小,中央经线无变形,自中央经线向投影带边缘,变形逐渐 增加,变形最大处在投影带内赤道的两端。按一定经差将地球椭球面划分成若干投影带,这是高斯投影中限制长度变形的最有效方法。
分带时既要控制长度变形使其不大于测图误差,又要使带数不致过多以减少换带计算工作,据此原则将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投 影。通常按经差6度或3度分为六度带或三度带。六度带自 0度子午线起每隔经差6度自西向东分带,带号依次编为第 1、2…60带。三度带是在六度带的基础上分成的,它的中央子午线与六度带的中央子午线和分带子午线重合,即自 1.5度子午线起每隔经差3度自西向东分带,带号依次编为三度带第 1、2…120带。我国的经度范围西起 73°东至135°,可分成六度带十一个,各带中央经线依次为75°、81°、87°、……、117°、123°、129°、135°,或三度带二十二 个。
我国大于等于50万的大中比例尺地形图多采用六度带高斯—克吕格投影,三度带高斯—克吕格投影多用于大比例尺1:1万测图,如城建坐标多采用三度带的高斯—克 吕格投影。高斯—克吕格投影按分带方法各自进行投影,故各带坐标成独立系统。以中央经线(L0)投影为纵轴X, 赤道投影为横轴Y,两轴交点即为各带的坐标原点。为了避免横坐标出现负值,高斯—克吕格投影北半球投影中规定将坐标纵轴西移500公里当作起始轴。由于高 斯—克吕格投影每一个投影带的坐标都是对本带坐标原点的相对值,所以各带的坐标完全相同,为了区别某一坐标系统属于哪一带,通常在横轴坐标前加上带号,如 (4231898m,21655933m),其中21即为带号。高斯—克吕格投影及分带示意图如下:
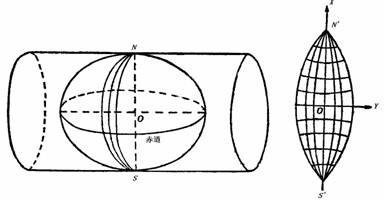
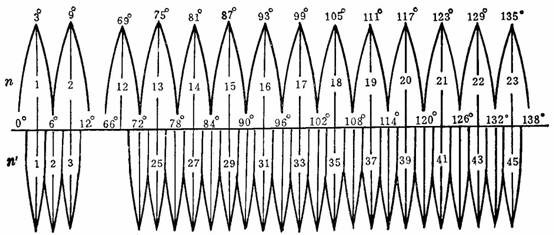
图8 高斯—克吕格投影及分带示意图
所谓动态投影指:改变ArcMap中的Data Frame(工作区)的空间参考或是对后加入到ArcMap工作区中数据的投影变换。ArcMap的Data Frame(工作区)的坐标系统默认为第一个加载到当前Data Frame(工作区)的那个文件的坐标系统,后加入的数据,如果和当前工作区坐标系统不同,则ArcMap会自动做投影变换,把后加入的数据投影变换到当前坐标系统下显示,但此时数据文件所存储的实际数据坐标值并没有改变,只是显示形态上的变化!因此叫动态投影。表现这一点最明显的例子就是在Export Data时,用户可以选择是按this layer‘s source data(数据源的坐标系统导出),还是按照the Data Frame(当前工作区的坐标系统)导出数据。
关于ArcMap的这种动态投影机制,我们可以利用一个北京54投影坐标系数据(乡镇.shp)和<ArcGIS Installation Directory>\DeveloperKit\SamepleCom\\data\World\目录下的world30.shp数据来做一个实验说明。
乡镇.shp数据的坐标系统为北京54投影坐标系(Krasovsky_1940_Transverse_Mercator)。在ArcMap或ArcCatalog中预览形态如图9所示:
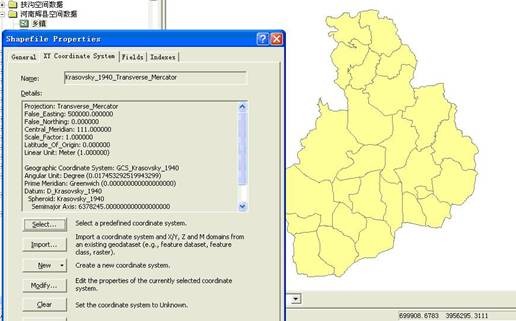
图9 北京54投影坐标系数据单独显示几何形态
world30.shp数据的坐标系统为WGS84坐标系(GCS_WGS_1984)。在ArcMap或ArcCatalog中预览形态如图10所示

图10 WGS84坐标系数据单独显示几何形态
而在ArcMap中先加载北京54坐标系数据后再加入WGS84坐标系数据,让ArcMap对WGS84坐标系数据进行动态投影后两数据叠加显示效果如图11所示:

图11 ArcMap对WGS84数据进行动态投影后的显示状态
可以非常明显的看到ArcMap对WGS84数据做完动态投影后的数据几何形态上的改变,并且此时从ArcMap右下角的状态栏上也可以看到当前Data Frame(工作空间)的坐标系统为北京54平面投影坐标系统。
反之在ArcMap中先加载WGS84坐标系数据后再加入北京54坐标系数据,让ArcMap对北京54坐标系数据进行动态投影后两数据叠加显示效果如图12所示:
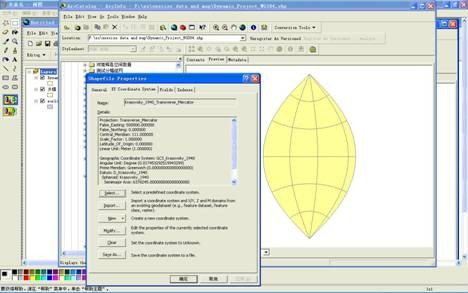
图12 ArcMap对北京54坐标系数据进行动态投影后的显示状态
将在图11中动态投影后的WGS84坐标系统数据按系统框架坐标系统导出后,单独加载或预览的数据几何形态如图13:
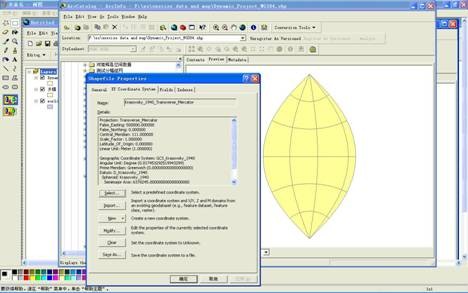
图13 按北京54坐标系统框架导出WGS84数据后的数据几何形态显示
ArcCatalog中数据定义坐标系统描述,即在数据上鼠标右键->Properties->XY Coordinate System选项卡,这里可以通过New、Modify、Select、Import方式来为数据定义坐标系统描述。但有许多用户都认为在这里定义了数据的坐标系统信息后,其数据本身就发生了投影变换。其实不然,这里定义的数据坐标系统信息都对应到与该数据同名而后缀名为.prj的文件当中!如果把该文件删除,在ArcCatalog中重新查看(要在该数据的上层节点上Refresh刷新一下)该文件的坐标信息时,一样会显示为Unknown,并且数据的坐标值并没有发生实质上的投影变换,这里改的仅仅是对数据坐标系统信息的一个描述而已,这就好比我们每个人的基本信息登记卡,更改了登记信息,但并没有改变你这个人本身。因此数据文件中所存储数据的坐标值并没有真正的投影变换到你想要更改到的坐标系统下。
我们同样拿上述的两个数据做一下实验,在ArcCatalog中更改world30.shp的坐标系统描述,在world30.shp文件上鼠标右键 ->Properties->XY Coordinate System选项卡中,通过Import方式导入乡镇.shp文件的Krasovsky_1940_Transverse_Mercator投影坐标系统描述,之后看一下结果图14。

图14 更改坐标系统描述后的数据几何形态
从上述示例我们可以很明显的看到更改数据的坐标系统描述并不能使数据做投影变换,从而使数据投影到平面上来,但该数据的prj文件已经记录了更改后的坐标系统描述,PROJCS["Krasovsky_1940_Transverse_Mercator",GEOGCS["GCS_Krasovsky_1940",DATUM["D_Krasovsky_1940",SPHEROID["Krasovsky_1940",6378245.0,298.3]],PRIMEM["Greenwich",0.0],UNIT["Degree",0.0174532925199433]],PROJECTION["Transverse_Mercator"],PARAMETER["False_Easting",500000.0],PARAMETER["False_Northing",0.0],PARAMETER["Central_Meridian",111.0],PARAMETER["Scale_Factor",1.0],PARAMETER["Latitude_Of_Origin",0.0],UNIT["Meter",1.0]]Prj文件记录了该投影坐标系的详细参数。
但对数据坐标系统的这个描述也是非常重要的,如果我们拿到一份数据,从ArcMap下所显示的坐标来看,像是投影坐标系统下的平面坐标,但不知道是基于哪个椭球体的什么投影方法,因此就无法再对数据做进一步的处理,如:投影变换、量测等操作。因为我们无法得知从什么坐标系统下开始变换,以及该坐标系统下的量测单位是什么。
因此大家一定要更正对ArcCatalog中数据属性中关于坐标系统描述的认识。
真正的投影变换。在ArcToolBox->Data Management Tools->Projections and Transformations中提供了如下工具:
在这个工具集下有这么几个工具最为常用:
1、Define Projection
2、Feature->Project
3、Raster->Project Raster
4、Create Custom Geographic Transformation
当数据在没有任何空间参考信息时,在ArcCatalog的坐标系统描述(XYCoordinate System)选项卡中会显示为Unknown!这时如果要对数据进行投影变换就要先利用Define Projection工具来给数据定义一个Coordinate System,然后再利用Feature->Project或Raster->Project Raster工具来对数据进行投影变换!
由于我们国家经常使用的坐标系统为北京54和西安80。这两个坐标系统变换到其他坐标系统下时,通常需要提供一个Geographic Transformation,因为不同投影所基于的椭球体及Datum不同!关键是Datum不同,也就是说当两个投影基于不同的Datum时就需要制定参数做Geographic Transformation。这里就用到我们前面所说的转换3参数、转换7参数了(三个平移参数ΔX、ΔY、ΔZ表示两坐标原点的平移值;三个旋转参数εx、εy、εz表示当地坐标系旋转至与地心坐标系平行时,分别绕Xt、Yt、Zt的旋转角;最后是比例校正因子,用于调整椭球大小),而我们国家的转换参数是保密的,因此可以自己计算或在购买数据时向国家测绘部门索要。
实际工作中一般都根据工作区内已知的北京54坐标控制点计算转换参数,如果工作区内有足够多的已知北京54与WGS84坐标控制点,可直接计算坐标转换所需的7参数或3参数;当工作区内有3个已知北京54与WGS84坐标控制点时,可用下式计算WGS84到北京54坐标的转换参数(A、B、C、D、E、F):
x54 = AX84 + BY84 + C
y54 = DX84 + EY84 + F
多余一点用作检验;在只有一个已知控制点的情况下(往往如此),用已知点的北京54与WGS84坐标之差作为平移参数,当工作区范围不大时精度也足够了。
精度要求较高,实测数据为WGS1984坐标数据时,欲转换到北京54基准面的高斯-克吕格投影坐标,如何定义坐标系参数呢?你可选择WGS 1984作为基准面,当只有一个已知控制点时,根据平移参数调整东伪偏移、北纬偏移值实现WGS84到 北京54的转换,此时的转换系数(A、B、C、D、E、F)中A、B、D、E为0,只有X、Y方向的平移值C、F ;当有3个已知控制点时,可利用得到的转换系数(A、B、C、D、E、F)定义 AffineTransform坐标系变换对象,实现坐标系的转换,当然有足够多已知控制点时,直接求定7参数自定义基准面就行了。
Geographic Transformation通常需要指定变换方向的,如果没有指定变换的方向,ArcMap会自动正确应用变换方法如从WGS 1984到 NAD1927,我们就可以选择NAD_1927_to_WGS_1984_3这种变换方法,ArcMap会自动判定转换方向从而正确实现数据的投影变换。有些变换方法是先把地理坐标系(经纬度)变换到地心坐标系(X Y Z),然后再将地心坐标系坐标(X Y Z),变换到地理坐标系统,图15。Geocentric Transformation(3参数)、Coordinate Frame(7参数)、Molodensky-Badekas(10参数,是7参数变换方法的一种变体,多了定义XYZ旋转轴的起始位置)都是这样的方法。
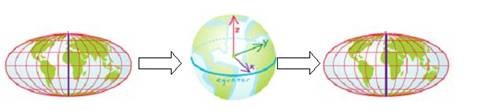
图15 从地理坐标系统变换到地心坐标系统再到地理坐标系统
Molodensky(3参数)和Abridged Molodensky(3参数是Molodensky方法的一种变体)变化方法则是直接在不同的地理坐标系统下进行变换无需借助地心坐标系进行转换。那么上述的这些方法的精度取决与用于定义转换参数的控制点的质量个数及选择的变换方法,精度相差可从厘米到米。
美国国家大地测量局用一种基于格网的变换方法(NADCON和HARN)在NAD1927和NAD1983及其他地理坐标系统下做变换,彼此相临的州的精度可达0.15米,阿拉斯加州及周边岛屿的精度可达0.5米,夏威夷地区精度可达0.2米等等,精度取决于计算栅格大小时测量数据的质量。随着卫星测距和测量技术的改善,美国在更新了测量控制网后,推出了这种High Accuracy Reference Network (HARN)方法或说是栅格格网,其精度可达0.05米。 加拿大采用同NADCON类似的基于格网的方法(NTV2)在NAD 1927 和 NAD 1983之间做变换,这种方法采用了双线性内插的方法来计算点的坐标。关于这两种方法本文不做更多描述,详细信息可参考ArcGIS帮助。
知道转换参数后,可以利用Create Custom Geographic Transformation工具来定义一个Geographic Transformation方法,变换方法可以根据已知的转换参数个数选择变换方法,这就完成了对数据的投影变换,数据本身坐标值就发生了变化。当然这种投影变换工作也可以在ArcMap中通过改变Data Frame的Coordinate System来实现,只是要在做完之后按照Data Frame的坐标系统导出数据即可,即为做“动态投影变换”。
相关的实验可选用ArcTutor(ArcDesktop中的练习数据)中的WGS84和NAD1927或NAD1983数据进行试验。
通过ArcToolBox->Data Management Tools->Projections and Transformations->Feature->Project可以实现两个坐标系之间的数据转换,如图16:
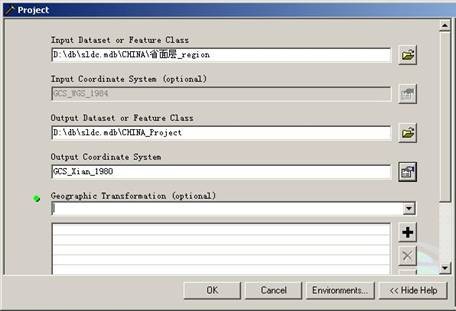
图16 投影转换
在选择好转换文件或数据集后,会自动显示文件或数据集所采用的坐标系统,选择转换后的坐标系统后,地理变换模板(Geographic Transformation)下拉框会自动加载可用的模板。如果没有可选项,只有用户自定义。
地理变换模板通过ArcToolBox->Data Management Tools->Projections and Transformations->Create Custom Geographic Transformation来创建,如图17:
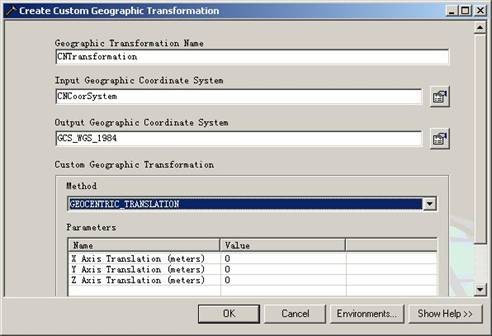
图17 自定义地理变换模板
其中,可用的转换方法有如下几种:
|
序号 |
方法名称 |
参数个数 |
含义 |
说明 |
|
1 |
GeoCentric_Translation |
3 |
地心偏移 |
参数越多,经度越高 |
|
2 |
MoloDensky |
3 |
|
|
|
3 |
MoloDensky_Abridged |
3 |
|
|
|
4 |
Position_Vector |
7 |
|
|
|
5 |
Coordinate_Frame |
7 |
|
|
|
6 |
MoloDensky_Badekas |
10 |
|
|
|
7 |
Nadcon |
1 |
格网变换 |
|
|
8 |
Harn |
1 |
|
|
|
9 |
Ntv2 |
1 |
|
|
|
10 |
Longitude_Rotation |
0 |
|
|
该文件在ArcGIS中对于CAD来说,是定义了2个点之间的相似变换的坐标对。即源点、目标点坐标值,一般来说源数据点的坐标是CAD图层上一个已知控制点(也可以是任意点)的坐标,而目标点的坐标值为想要该已知点重新定位到的坐标值。
CAD的world files文件是一个以wld为后缀的文本文件。因此我们可以用记事本或写字板任意创建或编辑world files文件,从而对CAD数据进行正确的配准和矫正。world file文件的示例如图18所示:
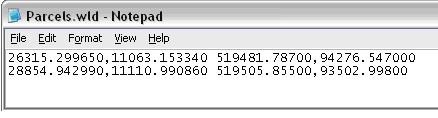
图18world file文件示例
CAD world file里的坐标对最多只有四对,即做一个2点的变换,world file文件既可以通过我们自己用文件编辑工具进行创建,同样ArcGIS也支持world file文件的创建与保存和加载等操作。在ArcMap中可以借助Georeferencing工具条的Add Contorl Point来增加控制点的映射关系(源和目标点),通过View Link Table打开Link Table对话框,利用Save工具按钮可以将建立好的Link关系保存成world file文件,或是使用Update Georeferencing菜单来保存Link关系从而生成world file文件。
一个CAD只能有一个world file文件,如果该数据集已经有了world file文件,则上述的Save或是Update Georeferencing操作将重写现有的world file文件。
ArcMap在加载CAD数据时,如果该数据有world file文件,ArcMap将使用world file所定义的转换关系对整个数据集的数据做变换。
影像数据的投影及坐标系统原理与矢量数据一致,只是因为其存储方式是以栅格行列形式存储的,因此需要将栅格数据与现实世界的坐标系建立起一个联系,因此部分影像数据也具有world file文件,之所以说部分影像具有world file文件是因为ERDAS, IMAGINE, BSQ, BIL, BIP, GeoTIFF和Grid影像是在其头文件中记录了数据的地理参考信息。
其他格式的影像则用一个独立的ASCII码的world file文件,其中记录着影像与real-world的坐标变换信息。其命名规范为文件名称与数据文件同名,后缀取影像格式后缀的第一第三个字符和w组成或直接在其后加‘w’字符,对于没有后缀或后缀不足3个字符的情况也采取在其命名后直接加‘w’表示,如图19所示:
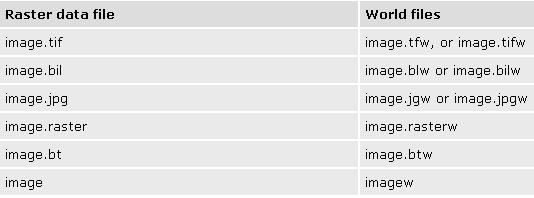
图19 world file文件命名示例
在ArcGIS 9.2 SP2中,如果无法用world file文件来记录这些变换信息,则Georeferencing 工具条的Update Georeferencing操作将把这些变换信息写进一个aux.xml文件中,并把这种仿射变换信息记录于一个文本文件中或是后缀扩展名以x结尾的文件中。如果对一个已经存在地图坐标系统信息的影像文件进行Update Georeferencing操作,则会生成一个以‘x’结尾的文件,用于记录真正的仿射变换信息(图20)。这个文件只需要把最后的‘x’字符删去,该文件便可在ArcGIS 9.1或是在没有ArcGIS软件的环境下使用。
图20 对已有坐标系统信息的影像进行world file命名的示例
影像文件的world file文件示例如下:
20.17541308822119
0.00000000000000
0.00000000000000
-20.17541308822119
424178.11472601280548
4313415.90726399607956
应用如下公式来表达image-to-world的6参数仿射变换
x1 = Ax + By + C
y1 = Dx + Ey + F
各参数意义如下:
X1、Y1待求的影像上某一像素的地理坐标
A、E分别为影像的每一像素点代表的X、Y方向上的分辨率
B、D旋转参数
C、F为影像左上角点的地理坐标值
通过上述6个参数,我们可以计算影像上任一像素点的真实地理坐标。这里 需要特别注意的一点是E参数之所以为负值,是由于影像坐标系和真实世界坐标系的Y轴方向相反,影像坐标的原点为影像左上角点,且Y轴正方向向下,而真实世界的坐标系统原点在左下角且Y轴正方向向上所致。影像数据的world file文件的制作和保存及Load操作跟CAD数据的world file文件方法相同,在此不敖述。
还需要注意的是ArcGIS会自动读取某些影像头文件(Geotiff)中的空间参考信息,从而会重写world file文件中的信息,因此可以设置选用world file文件来定义影像的坐标系统,通过勾选Tools->Options->Raster->General选项卡下的Use world file to define the coordinates of the raster选项即可。
本文转载自:http://blog.csdn.net/jax_lee/article/details/6764516
原文:http://www.cnblogs.com/wicked-fly/p/4736810.html