前言:
理论部分没写完+很不严谨……民那桑将就着看吧……以后有空补充……
数论部分详细参考任何一本数论教材。
同理,组合数学部分详细参考任何一本组合数学教材。
mobius函数 μ(x) 定义为
= (-1)r 【n = p1×p2×p3... ×pr,其中pi为不同的素数】
μ(x) = 1 【n = 1】
= 0 【其他,比方说 n = 4 = 22】
积性函数:
对于任意互素的正整数a,b,均有f(ab) = f(a) f(b), 则f为积性函数。
如:φ(x) 欧拉函数,μ(x) mobius函数。
完全积性:
对于任意正整数a,b,均有f(ab) = f(a) f(b), 则f为完全积性函数。
如:Legendre符号——
[B99.jpg)
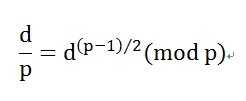 (此处为本人不严谨地说明……
)
(此处为本人不严谨地说明……
)
重要结论:
1. Σd|nφ(d)=n
2. Σd|nμ(d) = 1 (n == 1)
[Σd|nμ(d) = 0 (n > 1)]
mobius反演公式:
F(n) = Σd|nf(d) ? f(n) = Σd|nμ(n/d)F(d) 【注:这里的F,f为数论函数……不是随便什么函数都可以的啊…… 不过一般在竞赛中用到的貌似就是欧拉函数+莫比乌斯函数……】
碎碎念:
其实mobius函数-1,1什么的就是容斥里面+x1 -x2 ...的那个系数,当然我的意思是如果和容斥挂钩的话——因为我本人一开始草草一看就是这么理解的……所以偏好把mobius看成容斥——封装得很好的容斥。
当然,其实完全不必把mobius看成是容斥的一部分——这样感觉好像它只是容斥的一个特例的样子。
但是,就算是作为数论函数来看,mobius函数也是很重要的,意义远不止是容斥原理。
比方说积性啊什么的。
但是有些acm题如果用mobius函数的话就比较不用想容斥里面+-什么的了。比方说求1≤a≤m && 1≤b≤n &&gcd(a,b) == 1的a,b的组合数的这种类型的题目。
据说mobius在acm竞赛中常用的写代码技巧是:线性筛选+分块
详细参考——"贾志鹏线性筛"。
先奉上普通的方法(就是根据定义写的):

1 int mobius(int n) {
2 int miu = 0;
3 if(n == 1) return 1;
4 for(int i = 2; i < sqrt(n); i++) {
5 if(n % i == 0) {
6 m *= -1;
7 int flag = 0;
8 while(n % i == 0) {
9 n /= i;
10 flag = 1;
11 }
12 if(flag)return 0;
13 }
14 }
15 if(n > 1) return m *= -1;
16 return m;
17 }
然后是用筛选法做的(自己根据定义写的……暂时没发现bug,而且还用此过了HDU 1695)

1 const int maxn = 100011;
2 int miu[maxn];
3 int prime[maxn];
4 void mobius() {
5 memset(prime,0,sizeof prime);
6 miu[1] = 1;
7 prime[1] = 0;
8 for(int i = 2; i<maxn; i++) {
9 if(prime[i] == 0) {
10 long long j = (long long )i*(long long )i;
11 for(; j<maxn; j+=i) {
12 if(prime[j] == 0)
13 prime[j] = i;
14 }
15 miu[i] = -1;
16 continue;
17 }
18
19 int n = i;
20 miu[i] = 1;
21 while(prime[n]!=0) {
22 int tp = prime[n];
23 int flag = 0;
24 while(n % tp == 0) {
25 flag++;
26 if(flag==2) {
27 miu[i] = 0;
28 break;
29 }
30 n /= tp;
31 }
32 miu[i] *= -1;
33 if(flag == 2 ) break;
34 }
35 if(n>1)miu[i] *= -1;
36 }
37 }
例子:
HDU 1695
题意:已知a,b,c,d,k,求有多少x,y满足a≤x≤b, c≤y≤d,使得gcd(x,y) = k。
然后本题a = c = 1.
公式计算部分参考"贾"论文…… [电脑上打数学公式简直作死……]
1. 可以用容斥+欧拉函数
2. 可以用莫比乌斯(mobius)反演

1 #include<iostream>
2 #include<cstdlib>
3 #include<cstring>
4 #include<cstdio>
5 #include<algorithm>
6 #include<cmath>
7 using namespace std;
8 const int maxn = 100011;
9 int miu[maxn];
10 int prime[maxn];
11 void mobius() {
12 memset(prime,0,sizeof prime);
13 miu[1] = 1;
14 prime[1] = 0;
15 for(int i = 2; i<maxn; i++) {
16 if(prime[i] == 0) {
17 long long j = (long long )i*(long long )i;
18 for(; j<maxn; j+=i) {
19 if(prime[j] == 0)
20 prime[j] = i;
21 }
22 miu[i] = -1;//cout<<"miu["<<i<<"]: "<<miu[i]<<endl;
23 continue;
24 }
25
26 int n = i;
27 miu[i] = 1;
28 //if(i == 30)cout<<"i:"<<i<<" prime["<<n<<"]: "<<prime[n]<<endl;
29 while(prime[n]!=0) {
30 // if(i == 30)
31 // cout<<"n:"<<n<<endl;
32 int tp = prime[n];
33 int flag = 0;
34 while(n % tp == 0) {
35 flag++;
36 if(flag==2) {
37 miu[i] = 0;
38 break;
39 }
40 n /= tp;
41 }
42 // if(i == 30)
43 // cout<<"n:"<<n<<"flag:"<<flag<<endl;
44 miu[i] *= -1;
45 if(flag == 2 ) break;
46 }
47 if(n>1)miu[i] *= -1;
48 //cout<<"miu["<<i<<"]: "<<miu[i]<<endl;
49 }
50 }
51 int main() {
52 #ifdef LOCALL
53 //freopen("in","r",stdin);
54 //freopen("out","w",stdout);
55 #endif
56 int a,b,c,d,k;
57 mobius();
58 //cout<<miu[100000];
59 int t;
60 // while(cin>>t)
61 // cout<<"miu["<<t<<"]:"<<miu[t]<<endl;
62 cin>>t;
63 for(int kase = 1; kase < t+1; kase ++) {
64 cin>>a>>b>>c>>d>>k;
65 if(k == 0) {
66 cout<<"Case "<<kase<<": "<<"0\n";
67 continue;
68 }
69 long long ans = 0,repeat = 0;
70 b /= k;
71 d /= k;
72 int a1 = b<d?b:d;
73 for(int i = 1; i<=a1; i++) {
74 ans += (long long)miu[i]*(b/i)*(d/i);
75 }
76 for(int i = 1; i<=a1; i++) {
77 repeat += (long long)miu[i]*(a1/i)*(a1/i);
78 }
79
80 cout<<"Case "<<kase<<": "<<ans-repeat/2<<"\n";
81 }
82 return 0;
83 }
BZOJ 2301
题意:题意:已知a,b,c,d,k,求有多少x,y满足a≤x≤b, c≤y≤d,使得gcd(x,y) = k。
100%的数据满足:1≤n≤50000,1≤a≤b≤50000,1≤c≤d≤50000,1≤k≤50000
和上一题比起来就是a,c不一定等于1。。。
首先,如果我们按照上题那样做,在思路上完全没有问题,然后BZOJ这题给了50s,其实我觉得怎么想都是想给这种方法一个活路……
公式为 answer = [1,b; 1, d] - [1,a-1; 1, d] - [1,b; 1, c-1] + [1,a-1; 1,c-1]
【[a,b;c,d]的意思为 x∈[a,b] && y∈[c,d]的gcd满足条件的组合数】
分析一下复杂度: 1. 筛选法初始化mobius
大概O(nlog(n)log(log(n)))……额
这是Eratosthenes筛选法的复杂度……
2. 最坏可能是 求x,y都属于[1 - n]的可能组合数 那就是 O(n)
3. 可能有多个测试数据…… 然后这个数据个数也有n这么多……
话说 n 是 50000啊!
也就是这样算,去除零头什么的,大概是 O(n*n) = O(25×108) —— 106≈ 1s, 2500*106 ≈ 2500s……
……这…… 果断活不成……
但是我还是试了试…… 果断超时
贴个超时代码~

1 #include<iostream>
2 #include<cstdlib>
3 #include<cstring>
4 #include<cstdio>
5 #include<algorithm>
6 #include<cmath>
7 using namespace std;
8 typedef long long LL;
9 const int maxn = 100011;
10 int p,nn,plen;
11 int miu[maxn];
12 int pri[maxn];
13 int prime[maxn];
14
15 void mobius() {
16 memset(pri,0,sizeof pri);
17 memset(prime,0,sizeof prime);
18
19 miu[1] = 1;
20 pri[1] = 0;
21 plen = 0;
22 for(int i = 2; i<maxn; i++) {
23 if(pri[i] == 0) {
24 prime[plen++] = i;
25 LL j = (LL )i*(LL )i;
26 for(; j<maxn; j+=i) {
27 if(pri[j] == 0)
28 pri[j] = i;
29 }
30 miu[i] = -1;
31 continue;
32 }
33
34 int n = i;
35 miu[i] = 1;
36 while(pri[n]!=0) {
37 int tp = pri[n];
38 int flag = 0;
39 while(n % tp == 0) {
40 flag++;
41 if(flag==2) {
42 miu[i] = 0;
43 break;
44 }
45 n /= tp;
46 }
47 miu[i] *= -1;
48 if(flag == 2 ) break;
49 }
50 if(n>1)miu[i] *= -1;
51 }
52 }
53
54 int main() {
55 #ifdef LOCALL
56 freopen("in","r",stdin);
57 //freopen("out","w",stdout);
58 #endif
59
60 mobius();
61 //cout<<miu[100000];
62 int t;
63
64 scanf("%d",&t);
65 int a,b,c,d,k;
66 while(t--) {
67 scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
68 LL ans = 0, rep = 0;
69 int a1 = b/k<d/k?b/k:d/k;
70 for(int i = 1; i <= a1; i ++) {
71 ans += (long long)miu[i]*(b/k/i)*(d/k/i);
72 }
73 a1 = a/k<c/k?a/k:c/k;
74 for(int i = 1; i <= a1;i++){
75 ans += (long long)miu[i]*((a-1)/k/i)*((c-1)/k/i);
76 }
77
78 a1 = (a-1)/k<d/k?(a-1)/k:d/k;
79
80 for(int i = 1; i <= a1; i++) {
81 rep += (long long)miu[i]*((a-1)/k/i)*(d/k/i);
82 }
83 a1 = (c-1)/k<b/k?(c-1)/k:b/k;
84 for(int i = 1; i <= a1;i++){
85 rep += (long long)miu[i]*((c-1)/k/i)*(b/k/i);
86 }
87 printf("%lld\n",(ans - rep));
88 }
89 return 0;
90 }
然后就要用到 此报告中的分块优化了……
详细参考POI XIV Stage.1 Queries Zap 解题报告:http://wenku.baidu.com/view/fbe263d384254b35eefd34eb.html
分块优化的思想说起来高大上,其实是这样的:
1. 注意平常的mobius ,在进行反演之后主要还是进行枚举:
,在进行反演之后主要还是进行枚举:
如求x∈[1,a], y∈[1,b]的gcd(x,y) = 1的全部组合数 (假设 a>b)
1 for(int i = 1; i<=b; i++) {
2 ans += (long long)miu[i]*(a/i)*(b/i);
3 }
我们需要枚举全部小于b的值 —— 用容斥的说法就是,需要枚举全部gcd(x,y)大于1小于d的可能组合。
2. 我们来看一个图:
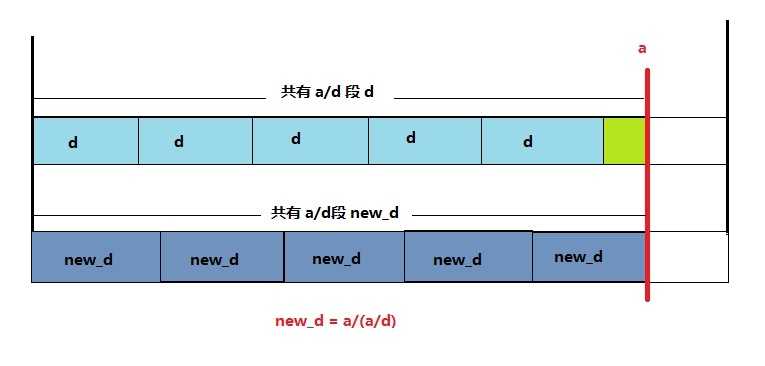
当gcd(x,y) = d (d > 1)时,我们可以看到,当gcd(x,y) 落在 [d, new_d]这段里时,a/gcd(x,y) 都等于 a/d。
就是凭借这个,我们可以进行分块优化。
因为 i = d 到 i = new_d 的这段都对应于(a/i)*(b/i),所以不用一个个求了,直接可以提取出"(a/i)*(b/i)"公因式,这样的话,只需要把μ(d)到μ(new_d)的值累加就好了,
因为需要μ的累加值,一开始我们也求出来[1,n]的μ值了,所以用前缀和的方法把所有的μ值的累加和先存起来……
嘛…… 这样优化了以后,算算复杂度:(具体复杂度推导过程,参看那篇POI解题报告+自己推算)
O(n*(2√(n/k) + 2√(n/k)) + n * √n) ≈ O(250000* √50000) ≈ O(250000* √50000) ≈ O(55*106) ≈ 50s
50s也就刚好差不了……
剧透一下:最后跑出来也就11+s而已…… 一开始还以为哪写差了,怎么这么久……(本人代码能力差……)然后随便搜了一个代码复制上去……居然也有10+s
……心理平衡了……
AC代码……

1 #include<iostream>
2 #include<cstdlib>
3 #include<cstring>
4 #include<cstdio>
5 #include<algorithm>
6 #include<cmath>
7 #define minum(a,b) (a)>(b)?(b):(a)
8 using namespace std;
9 typedef long long LL;
10 const int maxn = 50011;
11 int miu[maxn];
12 int pri[maxn];
13 int p[maxn];
14
15 void mobius() {
16 memset(pri,0,sizeof pri);
17
18 miu[1] = 1;
19 pri[1] = 0;
20 for(int i = 2; i<maxn; i++) {
21 if(pri[i] == 0) {
22 LL j = (LL )i*(LL )i;
23 for(; j<maxn; j+=i) {
24 if(pri[j] == 0)
25 pri[j] = i;
26 }
27 miu[i] = -1;
28 continue;
29 }
30
31 int n = i;
32 miu[i] = 1;
33 while(pri[n]!=0) {
34 int tp = pri[n];
35 int flag = 0;
36 while(n % tp == 0) {
37 flag++;
38 if(flag==2) {
39 miu[i] = 0;
40 break;
41 }
42 n /= tp;
43 }
44 miu[i] *= -1;
45 if(flag == 2 ) break;
46 }
47 if(n>1)miu[i] *= -1;
48 }
49 }
50 LL sum(int a,int b) {
51 int a1 = minum(a,b);
52 LL ans = 0;
53 int new_i;
54 for(int i = 1,new_i = 0; i <= a1; i = new_i + 1) {
55 new_i = minum(a/(a/i),(b/(b/i)));
56 ans += (LL)(p[new_i] - p[i-1])*(a/i)*(b/i);
57 }
58 return ans;
59 }
60 int main() {
61 #ifdef LOCALL
62 freopen("in","r",stdin);
63 //freopen("out","w",stdout);
64 #endif
65 mobius();
66 p[0] = 0;
67 for(int i = 1; i<maxn; i++) p[i] = p[i-1] + miu[i];
68 int t;
69 scanf("%d",&t);
70 int a,b,c,d,k;
71 while(t--) {
72 scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
73 printf("%lld\n",sum(b/k,d/k) - sum((a-1)/k,d/k) - sum(b/k,(c-1)/k) + sum((a-1)/k,(c-1)/k));
74 }
75 return 0;
76 }
(BTW, BZOJ 的 C++交cin | cout 会 RE …… )
)
还有啊……mobius反演可以用于求可重复的圆周排……
不过……可能由于我代码能力的问题…… 用mobius写就总是超时……待我写过了再来补充吧……呵呵呵呵呵……
还有啊…… 写这么多……好累啊……
原文:http://www.cnblogs.com/PeanutPrince/p/3619694.html