Description
Input
Output
For
each test case output on a single line the minimum number of moves
required to get all three pieces onto the same location, or the word
"impossible" if that is not possible for the given board and starting
locations. Sample Input
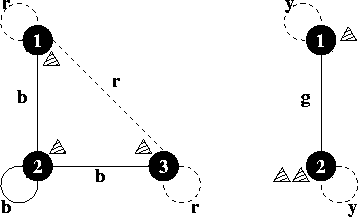
3 1 2 3 r b r b b b r b r 2 1 2 2 y g g y 0
Sample Output
2 impossible
题目大意：一张完全图，三个人，图的边上有颜色，三个人的位置已知，每次只能让一个人移动一次，求总共最少移动多少次，三个人能碰面。移动的规则是：当前人要走的边的颜色与其他两个人之间的边的颜色相同时，才能移动。
题目分析：大水题！！！wa了几次都是因为没有搞懂移动规则，把这道题记下来给自己涨个记性！！！
代码如下：
1 # include<iostream> 2 # include<cstdio> 3 # include<queue> 4 # include<cstring> 5 # include<algorithm> 6 using namespace std; 7 struct node 8 { 9 int a,b,c,t; 10 node(int _a,int _b,int _c,int _t):a(_a),b(_b),c(_c),t(_t){} 11 bool operator < (const node &a) const { 12 return t>a.t; 13 } 14 }; 15 int n,vis[60][60][60]; 16 char p[60][60]; 17 void bfs(int a,int b,int c) 18 { 19 priority_queue<node>q; 20 memset(vis,0,sizeof(vis)); 21 vis[a][b][c]=1; 22 q.push(node(a,b,c,0)); 23 while(!q.empty()) 24 { 25 node u=q.top(); 26 q.pop(); 27 if(u.a==u.b&&u.b==u.c&&u.a==u.c){ 28 printf("%d\n",u.t); 29 return ; 30 } 31 for(int i=1;i<=n;++i){ 32 if(p[u.a][i]==p[u.b][u.c]&&!vis[i][u.b][u.c]){ 33 vis[i][u.b][u.c]=1; 34 q.push(node(i,u.b,u.c,u.t+1)); 35 } 36 } 37 for(int i=1;i<=n;++i){ 38 if(p[u.b][i]==p[u.a][u.c]&&!vis[u.a][i][u.c]){ 39 vis[u.a][i][u.c]=1; 40 q.push(node(u.a,i,u.c,u.t+1)); 41 } 42 } 43 for(int i=1;i<=n;++i){ 44 if(p[u.c][i]==p[u.a][u.b]&&!vis[u.a][u.b][i]){ 45 vis[u.a][u.b][i]=1; 46 q.push(node(u.a,u.b,i,u.t+1)); 47 } 48 } 49 } 50 printf("impossible\n"); 51 } 52 int main() 53 { 54 int a,b,c; 55 while(scanf("%d",&n)&&n) 56 { 57 scanf("%d%d%d",&a,&b,&c); 58 for(int i=1;i<=n;++i) 59 for(int j=1;j<=n;++j) 60 cin>>p[i][j]; 61 bfs(a,b,c); 62 } 63 return 0; 64 }
POJ-2415 Hike on a Graph （BFS）
原文：http://www.cnblogs.com/20143605--pcx/p/4737109.html