Description

Input
Output
Sample Input
Sample Output
因为已知欧几里得算法gcd(a,b)=gcd(b,a%b) 所以x*a+y*b=gcd(a,b)=gcd(b,a%b)=x*b+y*a%b=x*b+y*(a-a/b*b)=y*a+(x-a/b*y)*b;
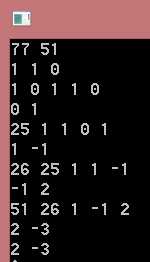
注意;a-a/b*b=a%b 这样就将a,b的线性组合化简b为a%b与的线性组合. 根据我的输出图可以看到: a,b都在减小,当b减小到0时, 我们就可以得出x=1,y=0; 然后递归回去就可以求出最终的x,y了
#include<iostream> using namespace std; void gcd(int a,int b,int & d,int &x,int &y) { if(!b) { d=a;x=1;y=0; // cout<<d<<" "<<x<<" "<<y<<endl; //输出 } else { gcd(b,a%b,d,y,x); // cout<<b<<" "<<a%b<<" "<<d<<" "<<y<<" "<<x<<endl; //输出 y-=a/b*x; // cout<<x<<" "<<y<<endl; //输出 } } int main() { int a,b,d,x,y; while(cin>>a>>b) { gcd(a,b,d,x,y); if(d!=1) cout<<"sorry"<<endl; else { while(x<0) //x不能小于0 x+=b,y-=a; cout<<x<<" "<<y<<endl; } } return 0; }
原文:http://www.cnblogs.com/hfc-xx/p/4737140.html