| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 2097 | Accepted: 448 | |
| Case Time Limit: 2000MS | ||
Description
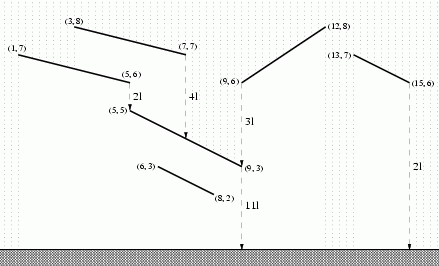
Input
Output
Sample Input
6 13 7 15 6 3 8 7 7 1 7 5 6 5 5 9 3 6 3 8 2 9 6 12 8
Sample Output
2 4 2 11 0 3
Source
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cmath>
#include <map>
#define N 41000
using namespace std;
struct num
{
int l,r,tl,tr;
__int64 sum;
}a[8*N],b[8*N];
struct Num
{
__int64 x1,y1,x2,y2;
int pos;
}c[N];
int x[2*N];
__int64 ans[N];
map<int,int>ma,ma1;
int w = 0;
bool cmp(Num p1,Num p2)
{
if(p2.x1>=p1.x1&&p2.x1<=p1.x2)
{
double y = (double)((p1.y2-p1.y1)*(p2.x1-p1.x1))/(p1.x2-p1.x1) + (double)p1.y1;
return y>(double)p2.y1;
}
if(p2.x2>=p1.x1&&p2.x2<=p1.x2)
{
double y = (double)((p1.y2-p1.y1)*(p2.x2-p1.x1))/(p1.x2-p1.x1) + (double)p1.y1;
return y>(double)p2.y2;
}
int k1 = min(p1.y1,p1.y2);
int k2 = min(p2.y1,p2.y2);
if(k1!=k2)
{
return k1>k2;
}else
{
return p1.x2<p2.x1;
}
}
int main()
{
//freopen("data.txt","r",stdin);
void build1(int k,int l,int r);
void build2(int k,int l,int r);
__int64 find1(int k,int l,int r);
__int64 find2(int k,int l,int r);
void update2(int k,int l,int val);
int n;
while(scanf("%d",&n)!=EOF)
{
for(int i=1;i<=n;i++)
{
scanf("%I64d %I64d %I64d %I64d",&c[i].x1,&c[i].y1,&c[i].x2,&c[i].y2);
c[i].pos = i;
x[2*i-1] = c[i].x1;
x[2*i] = c[i].x2;
}
sort(c+1,c+n+1,cmp);
sort(x+1,x+2*n+1);
int Top = 0;
ma.clear();
ma1.clear();
for(int i=1;i<=2*n;i++)
{
int k = x[i];
if(ma[k]==0)
{
ma[k]=++Top;
ma1[Top] = k;
}
}
build1(1,1,Top);
build2(1,1,Top);
for(int i=1;i<=n;i++)
{
__int64 res1 = find1(1,c[i].x1,c[i].x2);
res1 = c[i].x2-c[i].x1-res1;
__int64 res2 =find2(1,c[i].x1,c[i].x2);
res1 = res1+res2;
if(c[i].y1>c[i].y2)
{
update2(1,c[i].x2,res1);
}else
{
update2(1,c[i].x1,res1);
}
ans[c[i].pos] = res1;
}
for(int i=1;i<=n;i++)
{
printf("%I64d\n",ans[i]);
}
}
return 0;
}
void build1(int k,int l,int r)
{
a[k].l = l; a[k].r = r;
a[k].tl = ma1[l]; a[k].tr = ma1[r];
a[k].sum = 0;
if(l+1==r)
{
return ;
}
int mid = (l+r)>>1;
build1(k<<1,l,mid);
build1(k<<1|1,mid,r);
}
void pushup1(int k)
{
a[k].sum = a[k<<1].sum+a[k<<1|1].sum;
}
__int64 find1(int k,int l,int r)
{
if(a[k].tl==l&&a[k].tr==r)
{
__int64 val = a[k].sum;
a[k].sum = r-l;
return val;
}
if(a[k].tl<=l&&a[k].tr>=r&&(a[k].sum==a[k].tr-a[k].tl))
{
return r-l;
}
__int64 sum;
if(a[k<<1].tr>=r)
{
sum = find1(k<<1,l,r);
}else if(a[k<<1|1].tl<=l)
{
sum = find1(k<<1|1,l,r);
}else
{
sum = find1(k<<1,l,a[k<<1].tr);
sum += find1(k<<1|1,a[k<<1|1].tl,r);
}
pushup1(k);
return sum;
}
void build2(int k,int l,int r)
{
b[k].l = l; b[k].r = r;
b[k].tl = ma1[l]; b[k].tr = ma1[r];
b[k].sum = 0;
if(l==r)
{
return ;
}
int mid = (l+r)>>1;
build2(k<<1,l,mid);
build2(k<<1|1,mid+1,r);
}
void pushup2(int k)
{
b[k].sum = b[k<<1].sum+b[k<<1|1].sum;
}
__int64 find2(int k,int l,int r)
{
if(b[k].tl==l&&b[k].tr==r)
{
__int64 val = b[k].sum;
b[k].sum = 0;
return val;
}
__int64 sum;
if(b[k].sum==0)
{
b[k<<1].sum = 0;
b[k<<1|1].sum = 0;
}
if(b[k<<1].tr>=r)
{
sum = find2(k<<1,l,r);
}else if(b[k<<1|1].tl<=l)
{
sum = find2(k<<1|1,l,r);
}else
{
sum = find2(k<<1,l,b[k<<1].tr);
sum +=find2(k<<1|1,b[k<<1|1].tl,r);
}
pushup2(k);
return sum;
}
void update2(int k,int l,int val)
{
if(b[k].tl ==l&&b[k].tr==l)
{
b[k].sum+=val;
return;
}
if(b[k].sum==0)
{
b[k<<1].sum = 0;
b[k<<1|1].sum = 0;
}
if(b[k<<1].tr>=l)
{
update2(k<<1,l,val);
}else if(b[k<<1|1].tl<=l)
{
update2(k<<1|1,l,val);
}
pushup2(k);
}
POJ 1765 November Rain,布布扣,bubuko.com
原文:http://blog.csdn.net/yongxingao/article/details/22516675