一、图的表示:
图分为有向图和无向图,表示方式有邻接表,邻接矩阵,十字链表三种表示方式。
1.1 邻接矩阵
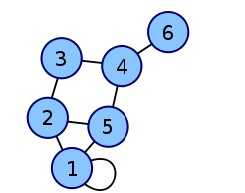

图1.1 图1.1对应的邻接矩阵
无向图的邻接矩阵是对称矩阵。
代码实现:
#include <stdio.h> #include <stdlib.h> /*#include <curses.h>*/ typedef char VertexType; //顶点类型应由用户定义 typedef int EdgeType; //边上的权值类型应由用户定义 #define MAXVEX 100 //最大顶点数,应由用户定义 #define INFINITY 65535 //用65535来代表无穷大 #define DEBUG typedef struct { VertexType vexs[MAXVEX]; //顶点表 EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边 int numVertexes, numEdges; //图中当前的顶点数和边数 }Graph; //定位 int locates(Graph *g, char ch) { int i = 0; for(i = 0; i < g->numVertexes; i++) { if(g->vexs[i] == ch) { break; } } if(i >= g->numVertexes) { return -1; } return i; } //建立一个无向网图的邻接矩阵表示 void CreateGraph(Graph *g) { int i, j, k, w; printf("输入顶点数和边数:\n"); scanf("%d,%d", &(g->numVertexes), &(g->numEdges)); #ifdef DEBUG printf("%d %d\n", g->numVertexes, g->numEdges); #endif for(i = 0; i < g->numVertexes; i++) { g->vexs[i] = getchar(); while(g->vexs[i] == ‘\n‘) { g->vexs[i] = getchar(); } } #ifdef DEBUG for(i = 0; i < g->numVertexes; i++) { printf("%c ", g->vexs[i]); } printf("\n"); #endif for(i = 0; i < g->numEdges; i++) { for(j = 0; j < g->numEdges; j++) { g->arc[i][j] = INFINITY; //邻接矩阵初始化 } } for(k = 0; k < g->numEdges; k++) { char p, q; printf("输入边(vi,vj)上的下标i,下标j和权值:\n"); p = getchar(); while(p == ‘\n‘) { p = getchar(); } q = getchar(); while(q == ‘\n‘) { q = getchar(); } scanf("%d", &w); int m = -1; int n = -1; m = locates(g, p); n = locates(g, q); if(n == -1 || m == -1) { fprintf(stderr, "there is no this vertex.\n"); return; } //getchar(); g->arc[m][n] = w; g->arc[n][m] = g->arc[m][n]; //因为是无向图,矩阵对称 } } //打印图 void printGraph(Graph g) { int i, j; for(i = 0; i < g.numVertexes; i++) { for(j = 0; j < g.numVertexes; j++) { printf("%d ", g.arc[i][j]); } printf("\n"); } } int main(int argc, char **argv) { Graph g; //邻接矩阵创建图 CreateGraph(&g); printGraph(g); return 0; }
1.2 邻接表
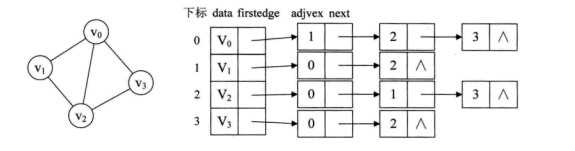
代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154 |
/* 邻接表表示的图结构 */#include <stdio.h>#include<stdlib.h> #define DEBUG#define MAXVEX 1000 //最大顶点数typedef
char VertexType; //顶点类型应由用户定义typedef
int EdgeType; //边上的权值类型应由用户定义 typedef
struct EdgeNode //边表结点{ int
adjvex; //邻接点域,存储该顶点对应的下标 EdgeType weigth; //用于存储权值,对于非网图可以不需要 struct
EdgeNode *next; //链域,指向下一个邻接点}EdgeNode; typedef
struct VertexNode //顶点表结构{ VertexType data; //顶点域,存储顶点信息 EdgeNode *firstedge; //边表头指针}VertexNode, AdjList[MAXVEX]; typedef
struct{ AdjList adjList; int
numVertexes, numEdges; //图中当前顶点数和边数}GraphList; int
Locate(GraphList *g, char
ch){ int
i; for(i = 0; i < MAXVEX; i++) { if(ch == g->adjList[i].data) { break; } } if(i >= MAXVEX) { fprintf(stderr,"there is no vertex.\n"); return
-1; } return
i;} //建立图的邻接表结构void
CreateGraph(GraphList *g){ int
i, j, k; EdgeNode *e; EdgeNode *f; printf("输入顶点数和边数:\n"); scanf("%d,%d", &g->numVertexes, &g->numEdges); #ifdef DEBUG printf("%d,%d\n", g->numVertexes, g->numEdges); #endif for(i = 0; i < g->numVertexes; i++) { printf("请输入顶点%d:\n", i); g->adjList[i].data = getchar(); //输入顶点信息 g->adjList[i].firstedge = NULL; //将边表置为空表 while(g->adjList[i].data == ‘\n‘) { g->adjList[i].data = getchar(); } } //建立边表 for(k = 0; k < g->numEdges; k++) { printf("输入边(vi,vj)上的顶点序号:\n"); char
p, q; p = getchar(); while(p == ‘\n‘) { p = getchar(); } q = getchar(); while(q == ‘\n‘) { q = getchar(); } int
m, n; m = Locate(g, p); n = Locate(g, q); if(m == -1 || n == -1) { return; } #ifdef DEBUG printf("p = %c\n", p); printf("q = %c\n", q); printf("m = %d\n", m); printf("n = %d\n", n); #endif //向内存申请空间,生成边表结点 e = (EdgeNode *)malloc(sizeof(EdgeNode)); if(e == NULL) { fprintf(stderr, "malloc() error.\n"); return; } //邻接序号为j e->adjvex = n; //将e指针指向当前顶点指向的结构 e->next = g->adjList[m].firstedge; //将当前顶点的指针指向e g->adjList[m].firstedge = e; f = (EdgeNode *)malloc(sizeof(EdgeNode)); if(f == NULL) { fprintf(stderr, "malloc() error.\n"); return; } f->adjvex = m; f->next = g->adjList[n].firstedge; g->adjList[n].firstedge = f; }} void
printGraph(GraphList *g){ int
i = 0; #ifdef DEBUG printf("printGraph() start.\n"); #endif while(g->adjList[i].firstedge != NULL && i < MAXVEX) { printf("顶点:%c ", g->adjList[i].data); EdgeNode *e = NULL; e = g->adjList[i].firstedge; while(e != NULL) { printf("%d ", e->adjvex); e = e->next; } i++; printf("\n"); }} int
main(int
argc, char
**argv){ GraphList g; CreateGraph(&g); printGraph(&g); return
0;} |
二 图的遍历
2.1深度优先搜索遍历DFS:
2.2广度优先搜索遍历BFS:
参考:
http://zh.wikipedia.org/wiki/%E5%9B%BE
http://blog.chinaunix.net/uid-26548237-id-3483650.html
原文:http://www.cnblogs.com/baozhilin/p/3633264.html