codeforces Round #320 (Div. 2) C. A Problem about Polyline(数学)

解题思路：

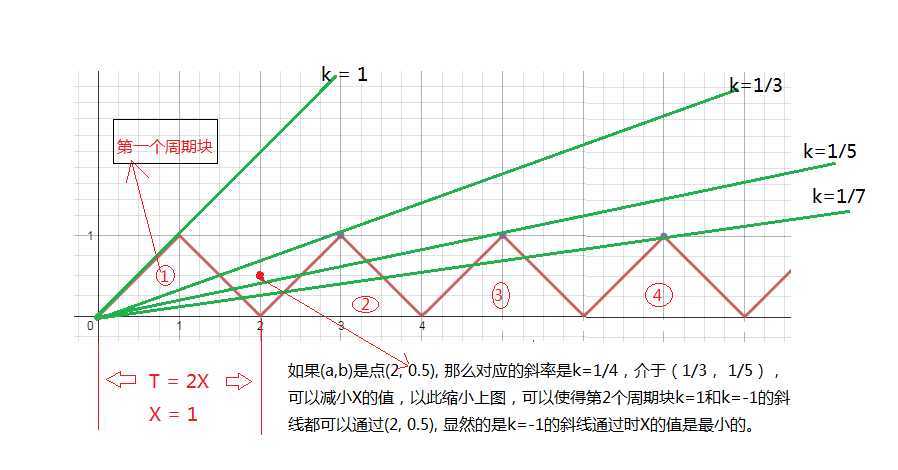
我们可以发现这样的一个规律：

(1)首先b一定要小于a，否则无论如何曲线也无法通过(a,b);

(2)设int k=a/b， 如果k为奇数，说明这个点在上图的绿色的线上， 没关系，我们让 k+=1；这样的话一定有(0,0), (a,b)这两点确定的直线的

斜率1/k介于(1/(k-1),  1/(k+1))之间，那么我们可以通过缩小（或者放大）X的值，使得第 k/2 个周期块 斜率为-1的那条边经过(a, b)。此时

的X值就是最小的！

(3)如果(a,b)在第 k/2 个周期块 斜率为-1的那条边上，那么这条边与X轴的交点就是(a+b, 0), 从(0, 0)到(a+b, 0)一共经过了 k/2个周期，

所以 X = (a+b)*1.0/(k/2 * 2)

(4)唉....想的这么明白，容易吗.....

#include <iostream>  
#include <algorithm>
#include<cstdio>
#include<cmath>
using namespace std;  
 
int main(){
    int a, b;
    cin>>a>>b;
     if(b>a) {
         cout<<-1<<endl;
     } else {
         int k = a/b;
         if(k&1) ++k;
         printf("%.12lf\n", (a+b)*1.0/k);
     }
    return 0;
}

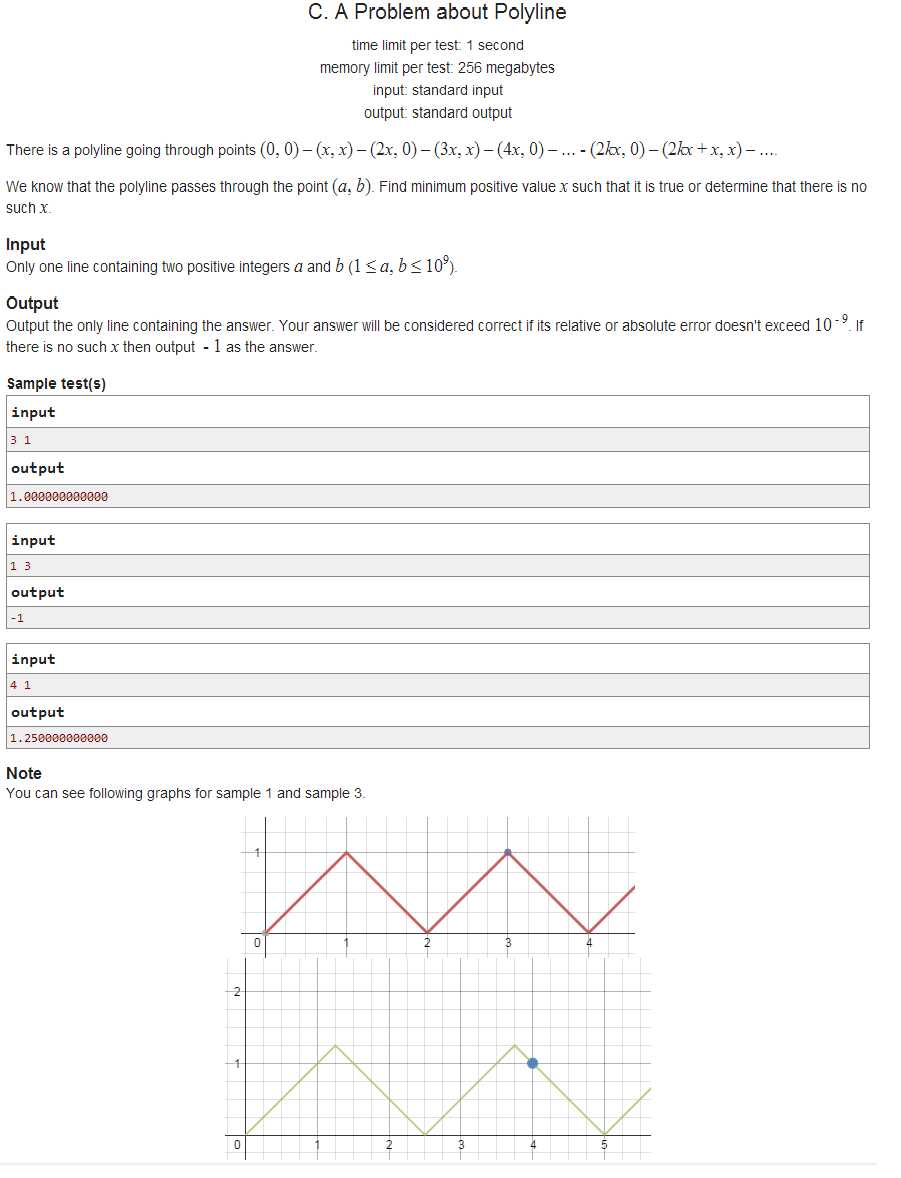
codeforces Round #320 (Div. 2) C. A Problem about Polyline(数学)

原文：http://www.cnblogs.com/hujunzheng/p/4826981.html