1. 快速排序的原理:
方法其实很简单:分别从初始序列"6 1 2 7 9 3 4 5 10 8"两端开始"探测"。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。这里可以用两个变量i和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字"哨兵i"和"哨兵j"。刚开始的时候让哨兵i指向序列的最左边(即i=1),指向数字6。让哨兵j指向序列的最右边(即=10),指向数字。
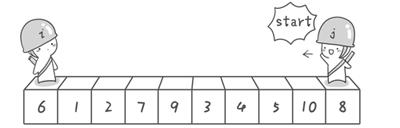
首先哨兵j开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵j先出动,这一点非常重要(请自己想一想为什么)。哨兵j一步一步地向左挪动(即j--),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前,哨兵i在了数字7面前。


现在交换哨兵i和哨兵j所指向的元素的值。交换之后的序列如下:
6 1 2 5 9 3 4 7 10 8


到此,第一次交换结束。接下来开始哨兵j继续向左挪动(再友情提醒,每次必须是哨兵j先出发)。他发现了4(比基准数6要小,满足要求)之后停了下来。哨兵i也继续向右挪动的,他发现了9(比基准数6要大,满足要求)之后停了下来。此时再次进行交换,交换之后的序列如下:
6 1 2 5 4 3 9 7 10 8
第二次交换结束,“探测”继续。哨兵j继续向左挪动,他发现了3(比基准数6要小,满足要求)之后又停了下来。哨兵i继续向右移动,糟啦!此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下:
3 1 2 5 4 6 9 7 10 8



到此第一轮"探测"真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。回顾一下刚才的过程,其实哨兵j的使命就是要找小于基准数的数,而哨兵i的使命就是要找大于基准数的数,直到i和j碰头为止。
OK,解释完毕。现在基准数6已经归位,它正好处在序列的第6位。此时我们已经将原来的序列,以6为分界点拆分成了两个序列,左边的序列是"3 1 2 5 4",右边的序列是"9 7 10 8"。接下来还需要分别处理这两个序列。因为6左边和右边的序列目前都还是很混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。现在先来处理6左边的序列现吧。
左边的序列是"3 1 2 5 4"。请将这个序列以3为基准数进行调整,使得3左边的数都小于等于3,3右边的数都大于等于3。好了开始动笔吧
如果你模拟的没有错,调整完毕之后的序列的顺序应该是:
2 1 3 5 4
OK,现在3已经归位。接下来需要处理3左边的序列"2 1"和右边的序列"5 4"。对序列"2 1"以2为基准数进行调整,处理完毕之后的序列为"1 2",到此2已经归位。序列"1"只有一个数,也不需要进行任何处理。至此我们对序列"2 1"已全部处理完毕,得到序列是"1 2"。序列"5 4"的处理也仿照此方法,最后得到的序列如下:
1 2 3 4 5 6 9 7 10 8
对于序列"9 7 10 8"也模拟刚才的过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列,如下
1 2 3 4 5 6 7 8 9 10
到此,排序完全结束。细心的同学可能已经发现,快速排序的每一轮处理其实就是将这一轮的基准数归位,直到所有的数都归位为止,排序就结束了。下面上个霸气的图来描述下整个算法的处理过程。

2. 快速排序代码实现:
1 package cn.itcast; 2 3 /* 4 * 快速排序: 5 * 一趟快速排序的算法是: 6 * 1)设置两个变量i、j,排序开始的时候:i=0,j=N-1; 7 * 2)以第一个数组元素作为关键数据,赋值给key,即 key=A[0]; 8 * 3)从j开始向前搜索,即由后开始向前搜索(j=j-1即j--), 9 * 找到第一个小于key的值A[j],A[i]与A[j]交换; 10 * 4)从i开始向后搜索,即由前开始向后搜索(i=i+1即i++), 11 * 找到第一个大于key的A[i],A[i]与A[j]交换; 12 * 5)重复第3、4、5步,直到 I=J; 13 * (3,4步是在程序中没找到时候j=j-1,i=i+1,直至找到为止。 14 * 找到并交换的时候i, j指针位置不变。 15 * 另外当i=j这过程一定正好是i+或j-完成的最后令循环结束。) 16 */ 17 public class QuickSort { 18 public static void sort(int[] data) { 19 quickSort(data, 0, data.length - 1); 20 } 21 22 private static void quickSort(int[] data, int i, int j) { 23 int pivotIndex = (i + j) / 2; 24 // swap 25 swap(data, pivotIndex, j); 26 27 int k = partition(data, i - 1, j, data[j]); 28 swap(data, k, j); 29 if ((k - i) > 1) 30 quickSort(data, i, k - 1); 31 if ((j - k) > 1) 32 quickSort(data, k + 1, j); 33 34 } 35 36 /** 37 * @param data 38 * @param i 39 * @param j 40 * @return 41 */ 42 private static int partition(int[] data, int l, int r, int pivot) { 43 do { 44 while (data[++l] < pivot) 45 ; 46 while ((r != 0) && data[--r] > pivot) 47 ; 48 swap(data, l, r); 49 } while (l < r); 50 SortTest.swap(data, l, r); 51 return l; 52 } 53 /* 54 * 交换数组中的两个元素 55 */ 56 public static void swap(int[] data, int i, int j) { 57 int temp = data[i]; 58 data[i] = data[j]; 59 data[j] = temp; 60 } 61 }
Java基础知识强化57:经典算法之快速排序(QuickSort)
原文:http://www.cnblogs.com/hebao0514/p/4834569.html