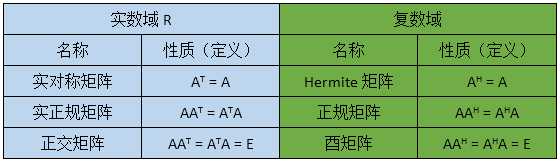
1.概述
我们先从实数域R开始说起,再延伸到复数域C上去,先列出一个表格,把实数域以及复数域中常见的矩阵及其性质概括如下:
表1 常见矩阵及其性质
我们知道实对称矩阵正交相似于对角阵,从而将一个方阵对角化,那么一个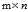 的矩阵能否对角化为对角阵呢,答案是肯定的,这也是奇异值分解(singular value decomposition,SVD)的意义所在。
的矩阵能否对角化为对角阵呢,答案是肯定的,这也是奇异值分解(singular value decomposition,SVD)的意义所在。
设A是一个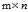 矩阵,则存在m阶正交矩阵U和n阶正交矩阵V,满足
矩阵,则存在m阶正交矩阵U和n阶正交矩阵V,满足
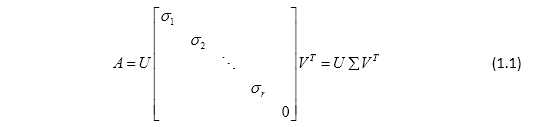
其中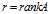 .习惯上,设
.习惯上,设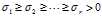 ,称
,称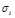 为奇异值(singular value),称U和V的前r列向量为奇异向量(singular vector),这个分解为奇异值分解。
为奇异值(singular value),称U和V的前r列向量为奇异向量(singular vector),这个分解为奇异值分解。
那现在就有疑问了,奇异值怎么求呢,m阶正交矩阵U和n阶正交矩阵V又怎么求呢,为了回答上述问题,我们将SVD写成向量形式,从而对SVD有初步的了解。令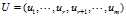 ,
,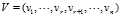 ,因为V是正交矩阵,所以有
,因为V是正交矩阵,所以有
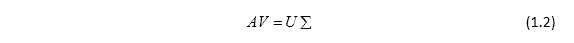
写成向量的形式有
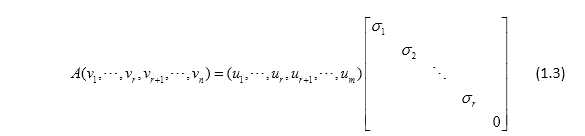
即
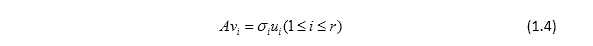
对1.1式转置得,
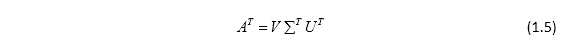
同理可得,
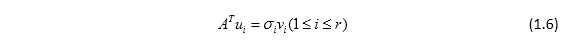
对1.4式两端左乘AT得,
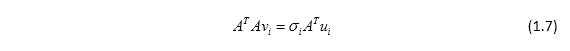
将1.6式代入1.7式中,
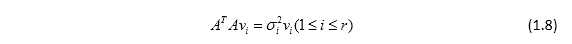
同理可得,
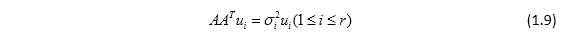
故vi是实对称矩阵ATA属于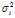 的特征向量,ui是实对称矩阵AAT属于
的特征向量,ui是实对称矩阵AAT属于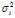 的特征向量。也就是说,奇异值就是实对称矩阵AAT(或者ATA)非零特征值的模长(即非零特征值开根号),而正交矩阵U(V)就是AAT(ATA)特征值所对应的特征向量。当然并不是随意地取m个特征向量组成U,随意地取n个特征向量组成V就可以构成A奇异值分解的正交矩阵的,U和V之间是配对的,有固定的关系,用表达式表示即为
的特征向量。也就是说,奇异值就是实对称矩阵AAT(或者ATA)非零特征值的模长(即非零特征值开根号),而正交矩阵U(V)就是AAT(ATA)特征值所对应的特征向量。当然并不是随意地取m个特征向量组成U,随意地取n个特征向量组成V就可以构成A奇异值分解的正交矩阵的,U和V之间是配对的,有固定的关系,用表达式表示即为
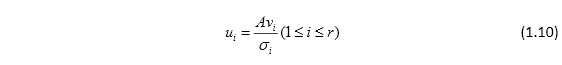
这个式子的推导在后面会介绍,现在继续探讨实对称矩阵AAT和 ATA特征值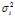 的性质,有如下两个性质:
的性质,有如下两个性质:
1)AAT和 ATA的特征值为非负数;
|
证明: 设
故 |
2)AAT和ATA的非零特征值集合相同;
|
证明: 假设A的秩为r,因为r(AAT) = r(AT),r(ATA) = r(A),且r(A) = r(AT),故 r(AAT) = r(ATA) = r(A) = r 因为AAT是实对称矩阵,所以 设
所以 |
因此,AAT和 ATA的特征值为非负数,且AAT和 ATA的非零特征值集合相同,即求A的奇异值时,只需求出AAT和ATA其中一个矩阵的特征值即可。
接下来,推导正交矩阵U和正交矩阵V之间的配对关系,设为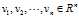 是n阶对称方阵ATA的单位正交特征向量,
是n阶对称方阵ATA的单位正交特征向量,
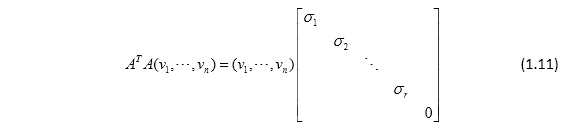
注意到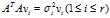 ,故
,故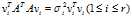 ,即
,即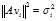 .令
.令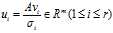 ,则
,则
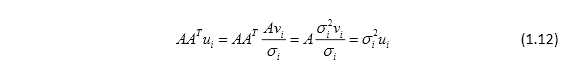
且有
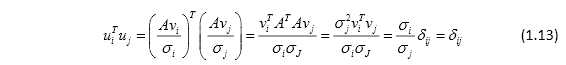
故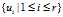 是AAT的单位正交特征向量。也就是说,当
是AAT的单位正交特征向量。也就是说,当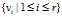 是ATA的单位正交特征向量时,
是ATA的单位正交特征向量时,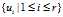 是AAT的单位正交特征向量,且
是AAT的单位正交特征向量,且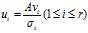 .
.
至此,矩阵A的奇异值分解就可以求出来了,首先求出AAT(ATA)的特征值,其中,非零特征值就是矩阵A的奇异值;接着求出AAT(ATA)特征值所对应的特征向量(包括零特征值对应的特征向量)作为正交矩阵U(V);最后根据配对关系求出另一个正交矩阵V(U)非零特征值所对应的特征向量,而正交矩阵V(U)的零特征值对应的特征向量则可以代入特征方程求出(或者其他方法),从而,得到任意矩阵A的奇异值分解。
这是实数域R的情况,复数域C中的奇异值分解大同小异。
设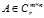 ,
,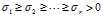 是A的r个奇异值,则存在m阶酉矩阵U和n阶酉矩阵V,满足
是A的r个奇异值,则存在m阶酉矩阵U和n阶酉矩阵V,满足
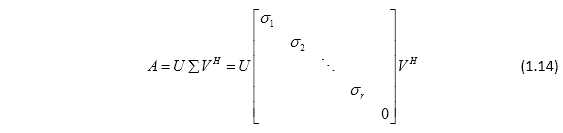
则上面的分解称为奇异值分解(复数域中)。
求任意一个复矩阵A的奇异值分解跟实矩阵A的奇异值分解步骤是一样的,就是非零特征值对应的次酉矩阵U1、V1的配对关系变为
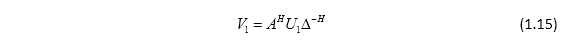
其中,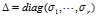 ,这是在求一个复矩阵A的奇异值分解时应该注意的。
,这是在求一个复矩阵A的奇异值分解时应该注意的。
2.例子
求矩阵
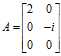
的奇异值分解表达式。
|
解: 步骤一:求出AAH和AHA的非零特征值(A的奇异值)
AAH的特征多项式为
AAH的特征值为 所以A的奇异值为 步骤二:求出AAH和AHA非零特征值对应的次酉矩阵U1和V1 AAH特征值为4的单位特征向量为
AAH特征值为1的单位特征向量为
所以AAH非零特征值对应的次酉矩阵U1为
因此,AHA非零特征值对应的次酉矩阵V1为
所以
|
3.应用
奇异值分解(SVD)的应用有特征降维(feature reduction)、图像压缩以及潜在语义分析(latent semantic indexing,LSI)等。就图像压缩来说,例如一张 的图像,需要
的图像,需要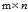 的矩阵来存储它。而利用奇异值分解,则只需存储矩阵的奇异值
的矩阵来存储它。而利用奇异值分解,则只需存储矩阵的奇异值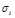 ,奇异向量
,奇异向量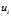 和
和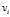 ,数目为
,数目为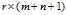 ,而不是
,而不是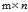 。通常
。通常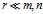 ,所以
,所以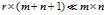 ,即存储该图像所需的存储量减小了。比值
,即存储该图像所需的存储量减小了。比值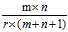 称为图像的压缩比,其倒数称为数据压缩率。如果矩阵的奇异值从一个数开始值远小于前面的奇异值,则可以删去,这样在保证图像不失真的前提下,进一步减小了存储量。
称为图像的压缩比,其倒数称为数据压缩率。如果矩阵的奇异值从一个数开始值远小于前面的奇异值,则可以删去,这样在保证图像不失真的前提下,进一步减小了存储量。
原文:http://www.cnblogs.com/xugenpeng/p/4839336.html