一、快速排序概述
关于快速排序,我之前写过两篇文章,一篇是写VC库中的快排函数,另一篇是写了快排的三种实现方法。现在再一次看算法导论,发现对快速排序又有了些新的认识,总结如下:
(1)、快速排序最坏情况下的时间复杂度为O(n^2),虽然最坏情况下性能较差,但快排在实际应用中是最佳选择。原因在于:其平均性能较好,为O(nlgn),且O(nlgn)记号中的常数因子较小,而且是稳定排序。
(2)、快速排序的思想和合并排序一样,即分治。快排排序的分治思想体现在:
a、首先从待排序的数中选择一个作为基数,基数的选择对于排序的性能有很大的影响,也是快排改进的关键所在。
b、分治,将比基数小的数放在左边,比基数大的数放在右边。
c、对分出来的两个分区分别执行上一步,直到区间只有一个数为止。
二、Hoare(霍尔)排序
快速排序首先由 C. A. R. Hoare(东尼霍尔,Charles Antony Richard Hoare)在1960年提出,之后又有许多人做了进一步的优化。
霍尔排序思路:采用数列第一个数作为基数,然后在数列的收尾两端分别设置两个“哨兵”,两个哨兵分别向中间探测比基数大、小的数,然后进行交换。如下图展示:
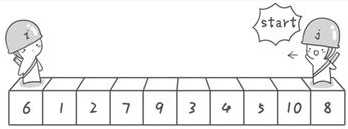
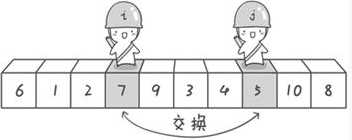
下面是霍尔排序的代码:
1 int Hoare_Partition(int arr[], int left, int right) 2 { 3 int temp = arr[left]; 4 int i = left; 5 int j = right; 6 7 while(i < j) { 8 while (arr[j] >= temp && i < j) //from right to left 9 j --; 10 while (arr[i] <= temp && i < j) //from left to right 11 i ++; 12 Swap(arr[i], arr[j]); 13 } 14 Swap(arr[left], arr[i]); 15 return i; 16 } 17 18 void Hoare_QuickSort(int arr[], int left, int right) 19 { 20 if (left < right) { 21 int mid = Hoare_Partition(arr, left, right); 22 Hoare_QuickSort(arr, left, mid-1); 23 Hoare_QuickSort(arr, mid+1, right); 24 } 25 }
三、算法导论讲述的快排
和霍尔排序不同的是,算法导论上实现的快排选取待排序数列的最后一个数作为基数,然后也设置两个哨兵,但这两个哨兵是从头到尾一起前进探测的。如果探测到一个数比基数小,就把该数移到左边,自然右边就成了最大的数了。代码如下:
1 int Partition(int arr[], int left, int right) 2 { 3 int temp = arr[right]; 4 int i = left - 1; 5 6 for (int j = left; j <= right-1; j ++) { 7 if (arr[j] <= temp) { 8 i ++; 9 Swap(arr[i], arr[j]); 10 } 11 } 12 Swap(arr[right], arr[i+1]); //!!!note: can‘t use temp:local variable 13 return i+1; 14 } 15 16 void QuickSort(int arr[], int left, int right) 17 { 18 if (left < right) { 19 int mid = Partition(arr, left, right); 20 QuickSort(arr, left, mid-1); 21 QuickSort(arr, mid+1, right); 22 } 23 }
四、快排的优化版本
如前所述,影响快排性能最大的因素在于基数的选取,虽然不管基数如何选取,算法最坏情况下时间复杂度都还存在,但能够减少常数项因子,从而优化了算法性能。下面引述下书上介绍的几种优化机制:
1、随机优化:
因为快排中Partition所产生的划分中可能会有”差的“,而划分的关键在于主元A[r]的选择。我们可以采用一种不同的、称为随机取样的随机化技术,把主元A[r]和A[p..r]中随机选出一个元素交换,这样相当于,我们的主元不在是固定是最后一个A[r],而是随机从p,...,r这一范围随机取样。这样可以使得期望平均情况下,Partition的划分能够比较对称。

2、中位数优化法:
所谓“三数取中”是指,从子数组中随机选出三个元素,取其中间数作为主元,这算是前面随机化版本的升级版。虽然是升级版,但是也只能影响快速排序时间复杂度O(nlgn)的常数因子。
3、递归栈的优化:
QUICKSORT算法包含两个对其自身的递归调用,即调用PARTITION后,左边的子数组和右边的子数组分别被递归排序。QUICKSORT中的第二次递归调用并不是必须的,可以用迭代控制结构来代替它,这种技术叫做“尾递归”,大多数的编译器也使用了这项技术。
模拟的尾递归:


代码实现:
1 //随机优化版本 2 //get random num between m and n; 3 int Random(int m, int n) 4 { 5 srand((unsigned int)time(0)); 6 int ret = m + rand() % (n-m+1); 7 return ret; 8 } 9 10 11 void Random_QuickSort(int arr[], int left, int right) 12 { 13 int index = Random(left, right); 14 15 Swap(arr[index], arr[right]); 16 QuickSort(arr, left, right); 17 }
1 //中位数优化,下面一个获取中位数的函数 2 //get mid num of a,b,c; 3 int MidNum(int a, int b, int c) 4 { 5 if ((a-b)*(a-c) <= 0) 6 return a; 7 else if ((b-a)*(b-c) <= 0) 8 return b; 9 else if ((c-a)*(c-b) <= 0) 10 return c; 11 }
1 //模拟尾递归 2 void Tail_Recursive_QuickSort(int arr[], int left, int right) 3 { 4 while (left < right) { //use while not if 5 int mid = Partition(arr, left, right); 6 Tail_Recursive_QuickSort(arr, left, mid-1); 7 left = mid + 1; 8 } 9 } 10 11 //尾递归优化 12 void Tail_Recursive_QuickSort_Optimize(int arr[], int left, int right) 13 { 14 while(left < right) { 15 int mid = Partition(arr, left, right); 16 if (mid-left < right-mid) { 17 Tail_Recursive_QuickSort_Optimize(arr, left, mid-1); 18 left = mid + 1; 19 } 20 else { 21 Tail_Recursive_QuickSort_Optimize(arr, mid+1, right); 22 right = mid - 1; 23 } 24 } 25 }
原文:http://www.cnblogs.com/bakari/p/4839109.html