简单二叉树
public class Node<T>
{
private T _data;
private Node<T> _leftChild;
private Node<T> _rightChild;
private Node<T> _Parent;
private int flag;
public Node(){}
public Node(T data) { this._data = data; flag = 0; }
public override string ToString()
{
return _data.ToString();
}
public T Data { get { return _data; } set { _data = value; } }
public Node<T> LeftChild { get { return _leftChild==null?null:_leftChild; } set { _leftChild = value; } }
public Node<T> RightChild { get { return _rightChild==null?null:_rightChild; } set { _rightChild = value; } }
public Node<T> Parent { get { return _Parent==null?null:_Parent; } set { _Parent = value; } }
public int Flag { get { return flag; } set { flag = value; } }
}
class BinaryTree<T>
{
private Node<T> _root;
public BinaryTree() { }
public BinaryTree(Node<T> node) { this._root = node; }
//四种序列
public Node<T> Root { get { return _root; } set { this._root = value; } }
}
层序遍历
public void ByLayerPrint()
{
Node<T> temp = new Node<T>();
Queue<Node<T>> queue = new Queue<Node<T>>();
queue.Enqueue(_root);
while (queue.Count > 0)
{
temp = queue.Dequeue();
Console.WriteLine(temp);
if (temp.LeftChild != null) { queue.Enqueue(temp.LeftChild); }
if (temp.RightChild != null) { queue.Enqueue(temp.RightChild); }
}
}
前序遍历
public void PreOrderPrint()
{
Node<T> temp = new Node<T>();
Stack<Node<T>> stack = new Stack<Node<T>>();
temp = _root;
while (temp != null || stack.Count > 0)
{
while (temp != null)
{
Console.WriteLine(temp);
stack.Push(temp);
temp = temp.LeftChild;
}
if (stack.Count > 0)
{
temp = stack.Pop();
temp = temp.RightChild;
}
}
}
中序遍历
public void InOrderPrint()
{
Node<T> temp = new Node<T>();
Stack<Node<T>> stack = new Stack<Node<T>>();
temp = _root;
while (temp != null)
{
stack.Push(temp);
temp = temp.LeftChild;
}
while (stack.Count > 0)
{
temp = stack.Pop();
Console.WriteLine(temp);
if (temp.RightChild != null) { stack.Push(temp.RightChild); }
}
}
后序遍历
public void PostOrderPrint()
{
Node<T> temp = new Node<T>();
Stack<Node<T>> stack = new Stack<Node<T>>();
temp = _root;
while (temp != null)
{
stack.Push(temp);
temp = temp.LeftChild;
}
while (stack.Count > 0)
{
temp = stack.Peek();
if (temp.RightChild == null || temp.RightChild.Flag == 1)
{
stack.Pop();
Console.WriteLine(temp);
temp.Flag = 1;
}
else
{
temp.Flag = 0;
temp = temp.RightChild;
while (temp != null)
{
stack.Push(temp);
temp = temp.LeftChild;
}
}
}
}
测试代码
static void Main(string[] args)
{
Node<string> node = new Node<string>("aaa");
Node<string> node2 = new Node<string>("bbb");
Node<string> node3 = new Node<string>("ccc");
Node<string> node4 = new Node<string>("ddd");
Node<string> node5 = new Node<string>("eee");
Node<string> node6 = new Node<string>("fff");
Node<string> node7 = new Node<string>("ggg");
Node<string> node8 = new Node<string>("hhh");
BinaryTree<string> tree = new BinaryTree<string>(node);
node.LeftChild = node5;
node.RightChild = node4;
node4.RightChild = node3;
node5.RightChild = node6;
node5.LeftChild = node7;
Console.WriteLine("******************************");
Console.WriteLine("******* 层序遍历 1 **********");
Console.WriteLine("******* 前序遍历 2 **********");
Console.WriteLine("******* 中序遍历 3 **********");
Console.WriteLine("******* 后序遍历 4 **********");
Console.WriteLine("******* 退出 0 **********");
Console.WriteLine("******************************");
while (true)
{
ConsoleKeyInfo key = Console.ReadKey();
switch (key.Key)
{
case ConsoleKey.D0:
Environment.Exit(0);
break;
case ConsoleKey.D1:
Console.WriteLine("---------层序遍历----------");
tree.ByLayerPrint();
break;
case ConsoleKey.D2:
Console.WriteLine("---------前序遍历----------");
tree.PreOrderPrint();
break;
case ConsoleKey.D3:
Console.WriteLine("---------中序遍历----------");
tree.InOrderPrint();
break;
case ConsoleKey.D4:
Console.WriteLine("---------后序遍历----------");
tree.PostOrderPrint();
break;
default:
Console.WriteLine("输入有误,重新输入");
break;
}
}
}
测试结果
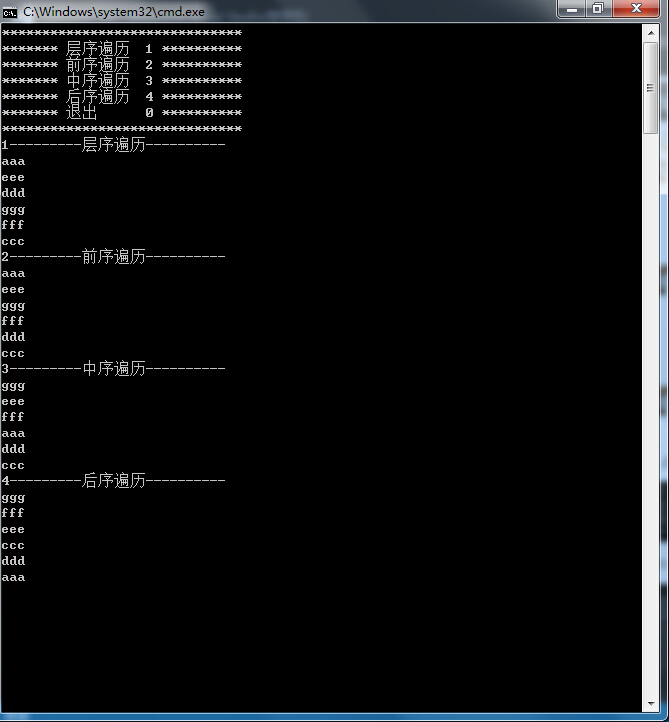
原文:http://my.oschina.net/hunjixin/blog/511498