条件概率
在机器学习算法中，我们可以发现概率论的知识无所不在，比如我们这里所讲的条件概率，提到条件概率不得不提贝叶斯公式，贝叶斯分类器的核心思想就是来自于条件概率，因此说，不懂数学原理，你是无法理解算法的核心思想的，也不知道算法能够解决什么样的问题。因此我们有必要把相关数学知识点拿出来复习一番。
条件概率所考虑的是在已知事件A发生的前提下求事件B发生的概率。举个简单的例子，抛硬币的例子，将一个硬币连续抛两次，假设事件A为至少出现一次正面的概率，事件B为两次一正一反的概率。求在事件发生的前提下，事件B发生的概率。我们知道事件的样本空间S={正正，正反，反正，反反}4种，A={正正，正反，反正}，所以P(A)=3/4，而B={正反，反正}，所以P(B)=2/4，而在A事件发生的前提下（也就是只存在正正，正反，反正3种情况），事件B发生的概率P(B|A)=2/3，事件A与事件B同时发生的概率P(AB)=2/4,从计算结果上看，2/3=(2/4)/(3/4),所以我们可以猜想P(B|A)=P(B)/P(A),或者P(B|A)=P(AB)/P(A)，两个公式。我们不妨把事件C定义为两次出现的结果一致，即C={正正，反反}，P(C|A)=1/3(只有正正满足条件)，P(AC)=1/4，P(C)=1/2，所以P(C|A)=P(AC)/P(A)。
这里我们猜测的计算公式为P(B|A)=P(AB)/P(A).
实际上，这个公式对一般的古典概型问题是成立的。为什么呢？我们假设实验的基本事件总数为n，A所包含的基本事件为m(m>0)，AB所包含的基本事件为k，则：
P(B|A)=k/m=(k/n)/(m/n)=P(AB)/P(A),其中P(B|A)就是在事件A发生的前提下事件B发生的概率，这就是条件概率。
如果B1,B2,B3……，是两两互不相容的事件（啥意思呢，就是说事件B可以分解为很多个小的事件，且任意两个小事件不重叠，用数学表达式描述为，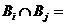
?），则有下面计算公式：
而对于一般性的事件B1和B2而言，则有：
公式中需要减去可能重叠的那一部分。
我们将公式转变一下，上面的公式是用除法表示的，换成乘法表示则有：
P(AB)=P(B|A)P(A).将该公式推广一下，如何求P(ABC)呢？
P(ABC)=P(C|AB)P(AB)=P(C|AB)P(B|A)P(A),再继续推广一下：
P(A1A2…An)=P(An|A1A2…An-1)P(An-1|A1A2…An-2)…P(A2|A1)P(A1)
下面我们介绍一下全概率的概念，并借此引出贝叶斯概率公式。
假设S为实验E的样本空间，而事件B1,B2,…Bn为一系列事件，且这些事件互不形容，且涵盖了整个样本空间S。即：
?，
。设事件A是E的事件（实际上事件A就是Bi中的一个或几个的组合形式而已）则有下面这个公式：
P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+…+P(A|Bn)P(Bn),Why?
简单证明一下，因为
,
因为Bi之间互不相容，所以
?，所以：
这就是全概率公式的计算，其实道理非常好理解。好了，我们现在将上式带入一开篇推倒的条件概率公式中。有：
这个就是贝叶斯公式。贝叶斯公式最大的作用的是将P(A|B)转化为P(B|A)的求解，而之所以这样是因为直接求解P(A|B)不好求，所以通过等价转换的方式转换到P(B|A)的形式，容易将问题的求解变得容易。
举个例子联系一下，对以往数据分析结果表明，当机器调整到良好状态时，产品的合格率是98%，当机器发生故障时，产品合格率为55%。每天开机时，机器处于良好状态的概率为95%，，试求一件产品是合格的时候，机器处于良好的状态的概率是多少？
解：设A为产品合格，B为机器状态良好，所以P(A|B)=98%,P(A|B*)=0.55(B*代表B的非)，P(B)=0.95,P(B*)=0.05,要求得问题是P(B|A).
利用贝叶斯概率公式求得
原文：http://my.oschina.net/dfsj66011/blog/511988