Write a function that takes an unsigned integer and returns the number of ’1‘ bits it has (also known as the Hamming weight).
For example, the 32-bit integer ’11‘ has binary representation 00000000000000000000000000001011, so the function should return 3.
解法1:考虑输入是无符号整数,而对其二进制表示右移即可判断最低位是0还是1;同时右移一位等价于除以2,因此可得最后循环结束条件。注意若没有限定无符号整数,在负数的时候可能引起死循环。运算次数与输入n最高位1的位置有关,最多循环32次。
class Solution { public: int hammingWeight(uint32_t n) { int cnt = 0; while(n) { cnt += n & 1; n >>= 1; } return cnt; } };
解法2:判断一个数的奇偶性即可推出其最后一位是0还是1,同时在辅以右移即可判断每一位的情况。
class Solution { public: int hammingWeight(uint32_t n) { int cnt = 0; while(n) { cnt += n % 2; n >>= 1; } return cnt; } };
解法3:判断二进制数某一位的情况可以利用与某个掩码的与来判断,初始时掩码unsigned int mask=0x01,然后逐次将mask左移一位。
class Solution { public: int hammingWeight(uint32_t n) { int cnt = 0; unsigned int mask = 0x01; while(mask) { if(n & mask) cnt++; mask <<= 1; } return cnt; } };
解法4:把一个整数减去1,再和原整数做与运算,会把该整数左右边的一个1变为0.因此该整数的二进制表示中有多少个1,就可以进行多少次这样的操作。运算次数与输入n的大小无关,只与n中1的个数有关。如果n的二进制表示中有k个1,那么这个方法只需要循环k次即可。
class Solution { public: int hammingWeight(uint32_t n) { int cnt = 0; while(n > 0) { cnt++; n = n & (n - 1); } return cnt; } };
解法5:查静态表。将0~15(4 bit)各个数中1的个数存储到表中,然后将输入整数按4位一段划分成多段,累计各段1的次数即可。也可以建立一个0~255(8 bit)或者16 bit甚至32 bit的表。
class Solution { public: int hammingWeight(uint32_t n) { unsigned int table[] = { 0,1,1,2, 1,2,2,3, 1,2,2,3, 2,3,3,4, }; int cnt = 0; while(n) { cnt += table[n & 0x0f]; n >>= 4; } return cnt; } };
class Solution { public: int hammingWeight(uint32_t n) { unsigned int table[256] = { 0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 4, 5, 5, 6, 5, 6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8, }; return table[n & 0xff] + table[(n >> 8) & 0xff] + table[(n >> 16) & 0xff] + table[(n >> 24) & 0xff]; } };
解法6:动态查表。由于表示在程序运行时动态创建的,所以速度上肯定会慢一些,把这个版本放在这里,有两个原因
1. 介绍填表的方法,因为这个方法的确很巧妙。
2. 类型转换,这里不能使用传统的强制转换,而是先取地址再转换成对应的指针类型。也是常用的类型转换方法。
class Solution { public: int hammingWeight(uint32_t n) { unsigned char BitsSetTable256[256] = {0} ; // 初始化表 for (int i = 0; i < 256; i++) BitsSetTable256[i] = (i & 1) + BitsSetTable256[i / 2]; unsigned int c =0 ; // 查表 unsigned char* p = (unsigned char*) & n ; c = BitsSetTable256[p[0]] + BitsSetTable256[p[1]] + BitsSetTable256[p[2]] + BitsSetTable256[p[3]]; return c ; } };
先说一下填表的原理,根据奇偶性来分析,对于任意一个正整数n
1.如果它是偶数,那么n的二进制中1的个数与n/2中1的个数是相同的,比如4和2的二进制中都有一个1,6和3的二进制中都有两个1。为啥?因为n是由n/2左移一位而来,而移位并不会增加1的个数。
2.如果n是奇数,那么n的二进制中1的个数是n/2中1的个数+1,比如7的二进制中有三个1,7/2 = 3的二进制中有两个1。为啥?因为当n是奇数时,n相当于n/2左移一位再加1。
再说一下查表的原理
对于任意一个32位无符号整数,将其分割为4部分,每部分8bit,对于这四个部分分别求出1的个数,再累加起来即可。而8bit对应2^8 = 256种01组合方式,这也是为什么表的大小为256的原因。
注意类型转换的时候,先取到n的地址,然后转换为unsigned char*,这样一个unsigned int(4 bytes)对应四个unsigned char(1 bytes),分别取出来计算即可。举个例子吧,以87654321(十六进制)为例,先写成二进制形式-8bit一组,共四组,以不同颜色区分,这四组中1的个数分别为4,4,3,2,所以一共是13个1,如下面所示。
10000111 01100101 01000011 00100001 = 4 + 4 + 3 + 2 = 13。
解法7:平行算法。先将n写成二进制形式,然后相邻位相加,重复这个过程,直到只剩下一位。以217(11011001)为例,217的二进制表示中有5个1:
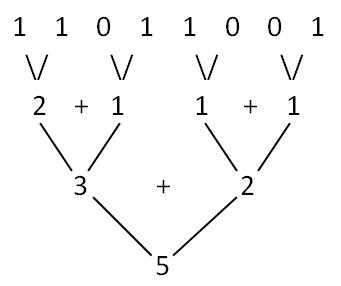
class Solution { public: int hammingWeight(uint32_t n) { n = (n & 0x55555555) + ((n >> 1) & 0x55555555) ; n = (n & 0x33333333) + ((n >> 2) & 0x33333333) ; n = (n & 0x0f0f0f0f) + ((n >> 4) & 0x0f0f0f0f) ; n = (n & 0x00ff00ff) + ((n >> 8) & 0x00ff00ff) ; n = (n & 0x0000ffff) + ((n >> 16) & 0x0000ffff) ; return n ; } };
解法8:
class Solution { public: int hammingWeight(uint32_t n) { unsigned int tmp = n - ((n >>1) &033333333333) - ((n >>2) &011111111111); return ((tmp + (tmp >>3)) &030707070707) %63; } };
最喜欢这个,代码太简洁啦,只是有个取模运算,可能速度上慢一些。区区两行代码,就能计算出1的个数,到底有何奥妙呢?为了解释的清楚一点,我尽量多说几句。
第一行代码的作用
先说明一点,以0开头的是8进制数,以0x开头的是十六进制数,上面代码中使用了三个8进制数。
将n的二进制表示写出来,然后每3bit分成一组,求出每一组中1的个数,再表示成二进制的形式。比如n = 50,其二进制表示为110010,分组后是110和010,这两组中1的个数本别是2和3。2对应010,3对应011,所以第一行代码结束后,tmp = 010011,具体是怎么实现的呢?由于每组3bit,所以这3bit对应的十进制数都能表示为2^2 * a + 2^1 * b + c的形式,也就是4a + 2b + c的形式,这里a,b,c的值为0或1,如果为0表示对应的二进制位上是0,如果为1表示对应的二进制位上是1,所以a + b + c的值也就是4a + 2b + c的二进制数中1的个数了。举个例子,十进制数6(0110)= 4 * 1 + 2 * 1 + 0,这里a = 1, b = 1, c = 0, a + b + c = 2,所以6的二进制表示中有两个1。现在的问题是,如何得到a + b + c呢?注意位运算中,右移一位相当于除2,就利用这个性质!
4a + 2b + c 右移一位等于2a + b
4a + 2b + c 右移量位等于a
然后做减法
4a + 2b + c –(2a + b) – a = a + b + c,这就是第一行代码所作的事,明白了吧。
第二行代码的作用
在第一行的基础上,将tmp中相邻的两组中1的个数累加,由于累加到过程中有些组被重复加了一次,所以要舍弃这些多加的部分,这就是&030707070707的作用,又由于最终结果可能大于63,所以要取模。
需要注意的是,经过第一行代码后,从右侧起,每相邻的3bit只有四种可能,即000, 001, 010, 011,为啥呢?因为每3bit中1的个数最多为3。所以下面的加法中不存在进位的问题,因为3 + 3 = 6,不足8,不会产生进位。
tmp + (tmp >> 3)-这句就是是相邻组相加,注意会产生重复相加的部分,比如tmp = 659 = 001 010 010 011时,tmp >> 3 = 000 001 010 010,相加得
001 010 010 011
000 001 010 010
---------------------
001 011 100 101
011 + 101 = 3 + 5 = 8。注意,659只是个中间变量,这个结果不代表659这个数的二进制形式中有8个1。
注意我们想要的只是第二组和最后一组(绿色部分),而第一组和第三组(红色部分)属于重复相加的部分,要消除掉,这就是&030707070707所完成的任务(每隔三位删除三位),最后为什么还要%63呢?因为上面相当于每次计算相连的6bit中1的个数,最多是111111 = 77(八进制)= 63(十进制),所以最后要对63取模。
参考:http://www.cnblogs.com/graphics/archive/2010/06/21/1752421.html
[LeetCode]8. Number of 1 Bits二进制表示中1的个数
原文:http://www.cnblogs.com/aprilcheny/p/4853079.html