PCA算法的步骤

① 样本矩阵X的构成

    假设待观察变量有M个属性，相当于一个数据在M维各维度上的坐标，我们的目标是在保证比较数据之间相似性不失真的前提下，将描述数据的维度尽量减小至L维（L<M）。

    样本矩阵X在这里用x 1 ,x 2 ,…,x N 共N个数据（这些数据都是以列向量的形式出现）来表示，那么X=[x 1  x 2  … x N ] MxN 。

② 计算样本X均值

    计算第m维（m=1,2,…,M）的均值如下：  

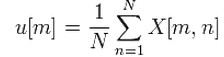
③ 计算观察值与均值的偏差

    在每一维上，用当前值X[m,n]减去u[m]，用矩阵运算表示如下：

    明显，h是一行向量，u是一列向量。

④ 计算协方差矩阵

    我们认为b i 代表B的第i行，那么由协方差矩阵

    推知 

    <>表示向量的内积，也就是每一项的积之和。

⑤ 计算协方差矩阵C的特征值和特征向量

    若XA=aA,其中A为一列向量，a为一实数。那么a就被称为矩阵X的特征值，而A则是特征值a对应的特征向量。    

    顺便扯一下，在matlab里面，求解上述A以及a，使用eig函数。如[D,V] = eig(C)，那么D就是n个列特征向量，而V是对角矩阵，对角线上的元素就是特征值。

⑥ 排序

    将特征值按 从大到小 的顺序排列，并根据特征值调整特征向量的排布。

    D’=sort(D);V’=sort(V);

⑦ 计算总能量并选取其中的较大值

    若V’为C的对角阵，那么总能量为对角线所有特征值之和S。

    由于在步骤⑥里面已对V进行了重新排序，所以当v’前几个特征值之和大于等于S的90%时，可以认为这几个特征值可以用来"表征"当前矩阵。

    假设这样的特征值有L个。

⑧ 计算基向量矩阵W

    实际上，W是V矩阵的前L列，所以W的大小就是 MxL 。

⑨ 计算z-分数（这一步可选可不选）

     Z[i,j]=B[i,j]/sqrt(D[i,i])

⑩ 计算降维后的新样本矩阵

     W * 表示W的转置的共轭矩阵，大小为 LxM , 而Z的大小为 MxN , 所以Y的大小为 LxN , 即降维为 N 个 L 维向量。

总结一下：

    去除平均值

    计算协方差矩阵

    计算协方差矩阵的特征值和特征向量

    将特征值从大到小排序

    保留最上面的N个特征值

 Python实现PCA算法源代码如下：

def pca(dataMat, topNfeat=9999999):
    meanVals = mean(data, axis=0) #求均值
    meanRemoved = dataMat - meanVals #去除均值
    covMat = cov(meanRemoved, rowvar=0)  #计算协方差
    eigVsls, eigVects = linalg.eig(mat(covMat)) #计算协方差矩阵的特征值和特征向量
    eigValInd = argsort(eigVals)  #特征值从大到小排序
    eigValInd = eigValInd[:-(topNfeat+1):-1]
    redEigVects = eigVects[:,eigValInd]
    lowDDateMat = meanRemoved * redFigVects #将数据转换到新的空间
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat 

Python实现PCA降维算法计算过程

原文：http://my.oschina.net/dfsj66011/blog/513665