当两个城市之间有安全的道路的时候,他们是互相可到达的,这种关系满足自反、对称和传递性,
因此是一个等价关系,在图论中就对应一个连通块。
在一个连通块中,当前点是那个并不影响往其他连通块的点连边,因此只要记录当前连通块内有哪些点。
n<=30,数组是开不下的,而且状态转移是很少的,只会向二进制1数量增加的方向转移,所以用map保存。(最极限的应该是是2^29...)
适合用记忆化搜索来写。
很容易想到的转移方程是
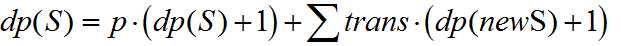
S表示当前所在连通块,p是向连通快内点走的概率,trans走向某个点的概率,newS表示走到当前连通块以外得到的新连通块。
如果直接用这个式子计算会无限递归的,做一点小小的变形就好了
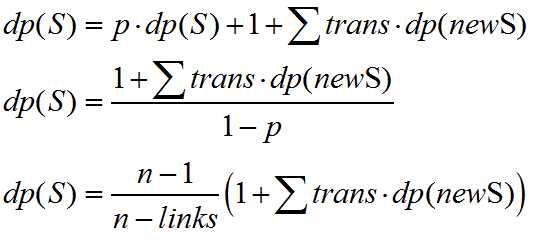
这样dp(S)的计算就不依赖dp(S)本身了。
#include<bits/stdc++.h> using namespace std; const int maxn = 30; int n,m; int pa[maxn]; int wei[maxn]; int fdst(int x) { return x == pa[x]? x : pa[x] = fdst(pa[x]); } void mrge(int x,int y) { int a = fdst(x), b = fdst(y); if(a != b){ pa[a] = b; wei[b] |= wei[a]; } } void initUF() { for(int i = 0; i < n; i++){ pa[i] = i; wei[i] = 1<<i; } } map<int,double> meo; map<int,double>:: iterator it; #define MP make_pair #define fi first #define se second double tr; double dp(int s) { if((it = meo.find(s)) != meo.end()) return it->second; double ans = 0; int lks = 0; for(int i = n; i--;){ if(s>>i&1) { lks++; continue; } ans += dp(s|wei[i]); } ans = (n-1.)/(n-lks)*(tr*ans + 1); meo.insert(MP(s,ans)); return ans; } //#define LOCAL int main() { #ifdef LOCAL freopen("in.txt","r",stdin); #endif int T, ks = 0; cin>>T; while(T--){ scanf("%d%d",&n,&m); printf("Case %d: ",++ks); if(n == 1){ puts("0"); continue; } initUF(); for(int i = m; i--; ){ int x,y; scanf("%d%d",&x,&y); mrge(x-1,y-1); } tr = 1./(n-1); for(int i = n; i--;){ wei[i] = wei[fdst(i)]; } meo.clear(); meo.insert(MP((1<<n)-1,0)); printf("%lf\n",dp(wei[0])); } return 0; }
原文:http://www.cnblogs.com/jerryRey/p/4857941.html