1 2 4 6
3 5 13 25
#include<cstdio>
const int N = 1000001;
int e[N];
__int64 a[N], res = 0;
void euler()
{
for(int i = 2; i < N; i++)
e[i] = 0;
e[1] = 1;
for(int i = 2; i < N; i++)
if(!e[i])
{
for(int j = i; j < N; j += i)
{
if(!e[j])
e[j] = j;
e[j] = e[j] / i * (i-1);
}
}
}
int main()
{
int i, n;
euler();
for(i = 1; i < N; i++)
{
res += e[i];
a[i] = res * 2 + 1;
}
while(~scanf("%d", &n))
printf("%I64d\n", a[n]);
return 0;
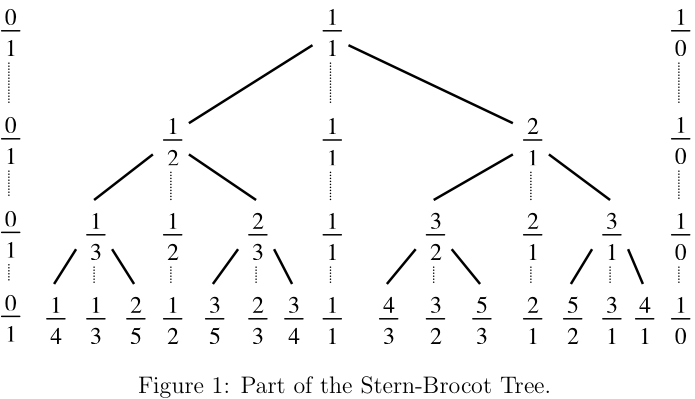
}hdu 4556 Stern-Brocot Tree,布布扣,bubuko.com
原文:http://blog.csdn.net/lyhvoyage/article/details/22889709