对于RB-tree,首先做一个了解,先看一张维基百科的RB-tree:
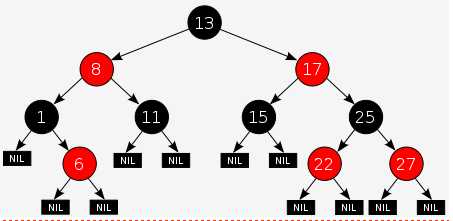
再看RB-tree的性质:
性质1. 节点是红色或黑色。 性质2. 根是黑色,所有叶子都是黑色(叶子节点指的是NIL节点)。。 性质3. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点) 性质4. 从任一节点到其每个叶子的所有简单路径 都包含相同数目的黑色节点。
在展开红黑树之前, 首先来看看普通二叉搜索树的插入和删除. 插入很容易理解, 比当前值大就往右走, 比当前值小就往左走。
这里详细展开的是删除操作:
二叉树的删除操作有一个技巧, 即在查找到需要删除的节点 X;
接着我们找到要么在它的左子树中的最大元素节点 M、要么在它的右子树中的最小元素节点 M, 并交换(M,X). 此时, M 节点必然至多只有一个孩子;
最后一个步骤就是用 M 的子节点代替 M 节点就完成了。
所以, 所有的删除操作最后都会归结为删除一个至多只有一个孩子的节点, 而我们删除这个节点后, 用它的孩子替换就好了. 将会看到 sgi stl map 就是这样的策略.
在红黑树删除操作讲解中, 我们假设代替 M 的节点是 N(下面的讲述不再出现 M).
插入新节点总是红色节点, 因为不会破坏性质 5, 尽可能维持所有性质.
假设, 新插入的节点为 N, N 节点的父节点为 P, P 的兄弟(N 的叔父)节点为 U, P 的父亲(N 的爷爷)节点为 G. 所以有如下的印象图:
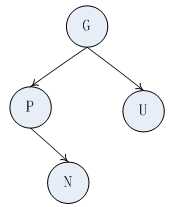
插入节点的关键是:
插入新节点总是红色节点 如果插入节点的父节点是黑色, 能维持性质 如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质
插入算法详解如下, 走一遍红黑树维持其性质的过程:
第 0.0 种情况, N 为根节点, 直接 N->黑. over
第 0.1 种情况, N 的父节点为黑色, 这不违反红黑树的五种性质. over
第 1 种情况, N,P,U 都红(G 肯定黑). 策略: G->红, N,P->黑. 此时, G 红, 如果 G 的父亲也是红, 性质又被破坏了, 这时,可以将 GPUN 看成一个新的红色 N 节点, 如此递归调整下去; 特殊的, 如果碰巧将根节点染成了红色, 可以在算法的最后强制 root->黑.
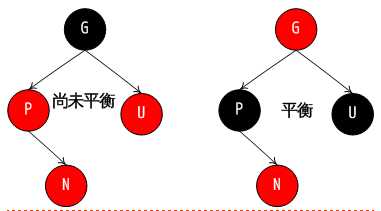
第 2 种情况, P 为红, N 为 P 右孩子, N 为红, U 为黑或缺少. 策略: 旋转变换, 从而进入下一种情况:(分N在P的左边还是右边)
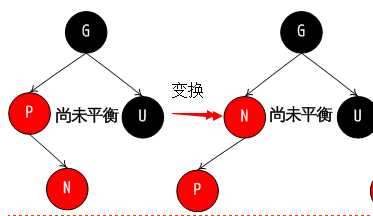
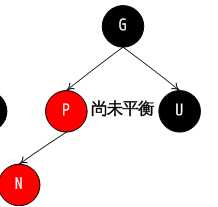
第 3 种情况, 可能由第二种变化而来, 但不是一定: P 为红, N 为 P 左孩子, N 为红. 策略: 旋转, 交换 P,G 颜色, 调整后, 因为 P 为黑色, 所以不怕 P 的父节点是红色的情况. over
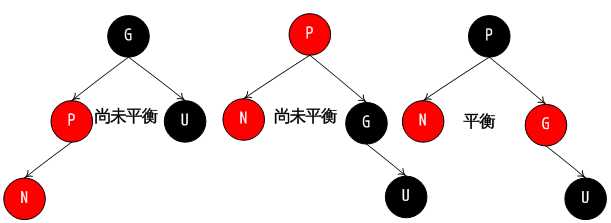
红黑树的插入就为上面的三种情况. 你可以做镜像变换从而得到其他的情况.
原文:http://www.cnblogs.com/stemon/p/4860625.html