




个人理解:
1、首先纠正上文一处错误,公式(16)下方的推导式存在笔误,虽然结论正确,但推导过程比较晦涩,数学基础不好的不易看懂。我在这里再把几个主要公式推导公式整理一下:
首先给出g(z)的求导过程:
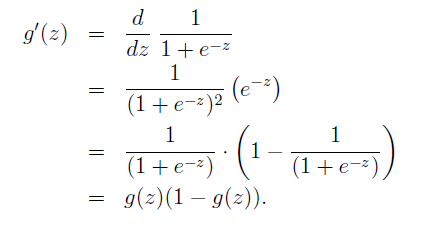
其次再给出似然函数:
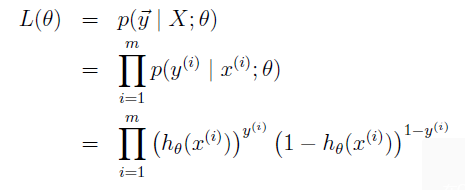
对似然函数取对数求解过程:

梯度下降求解过程中求导步骤:

2、过拟合与欠拟合的理解:过拟合就是过分的与训练集追求完美导致对于训练集外的测试数据适应不了,事实证明m个样本总会有m-1阶的函数完美拟合,比如直线(一阶)能完美通过两个样本,三个点可以被二阶抛物线完美拟合。所以说当你有7个训练集时你可以用六阶函数完美拟合,当增加一个训练样本时,为了再次调整函数模型,你需要一个七阶函数,显然差了很多。欠拟合就是很次的拟合训练集,明显也不符合数据规律。
3、参数学习算法与非参数学习算法的基本概念了解一下就可以了,不要想当然的认为非参数学习算法是没有参数的算法就好,其实整个机器学习,学习的到底是什么,我个人认为就是参数的学习,没有个参数,还学啥,当一切都是定数,那就成严格的数学定理了,带公式计算,结果是一定的。
4、局部加权线性回归的主要思想(纯粹个人理解)是认为数据集中的数据是“连续的”,这些数据可以被一条曲线很好的拟合,而我们做的是直线型模型,怎样使直线型模型得出一个曲线?就是对曲线中的点求导,也就是切线,所以说我们认为预测点周围的点的权重较大是因为预测点周围的点可以被该点的切线近似直线拟合,而远离该点的值几乎不被切线经过,所以权值为0,也就是不考虑远离它的点。
5、上一篇文章我们提到过为什么采用最小二乘而不是三乘或一乘等,上文已经给出解释,主要是基于最大似然估计给出的,如果有对最大似然估计不清楚的朋友,可以参考我的另一篇文章最大似然估计。
6、上面提到的算法都属于广义的线性回归,后面会讲到,所以它们的公式看起来好像一样,这也正说明了一种通用性,而不是巧合,后面会证明。
原文:http://my.oschina.net/dfsj66011/blog/515028