On a plane are n points (xi, yi) with integer coordinates between 0 and 106. The distance between the two points with numbers a and bis said to be the following value: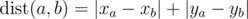 
(the distance calculated by such formula is called Manhattan distance).
We call a hamiltonian path to be some permutation pi of numbers from 1 to n. We say that the length of this path is value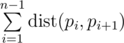 
.
Find some hamiltonian path with a length of no more than 25 × 108. Note that you do not have to minimize the path length.
The first line contains integer n (1 ≤ n ≤ 106).
The i + 1-th line contains the coordinates of the i-th point: xi and yi (0 ≤ xi, yi ≤ 106).
It is guaranteed that no two points coincide.
Print the permutation of numbers pi from 1 to n — the sought Hamiltonian path. The permutation must meet the inequality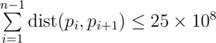 
.
If there are multiple possible answers, print any of them.
It is guaranteed that the answer exists.
5
0 7
8 10
3 4
5 0
9 12
4 3 1 2 5
In the sample test the total distance is:
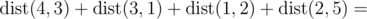
(|5 - 3| + |0 - 4|) + (|3 - 0| + |4 - 7|) + (|0 - 8| + |7 - 10|) + (|8 - 9| + |10 - 12|) = 2 + 4 + 3 + 3 + 8 + 3 + 1 + 2 = 26
题意：给你一个1e6*1e6的图，上面有n个点，定义dist距离，求一条任意路径使得dist总和不超过 25*1e8
题解：分块思想，讲1e6分成1000份，x(1000*(k-1)<=x<=1000*k)每份对y单调递增，对于一份，在y轴上产生价值最多1e6，1000份就是1e9.
在x轴上，假设所有点分布在一份上，则最多是1e9，如果任意分布最多也是1e9
总的来说就是2*1e9，可行
///1085422276 #include<bits/stdc++.h> using namespace std ; typedef long long ll; #define mem(a) memset(a,0,sizeof(a)) #define meminf(a) memset(a,127,sizeof(a)); #define TS printf("111111\n"); #define FOR(i,a,b) for( int i=a;i<=b;i++) #define FORJ(i,a,b) for(int i=a;i>=b;i--) #define READ(a,b,c) scanf("%d%d%d",&a,&b,&c) #define inf 100000 inline ll read() { ll x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘) { if(ch==‘-‘)f=-1; ch=getchar(); } while(ch>=‘0‘&&ch<=‘9‘) { x=x*10+ch-‘0‘; ch=getchar(); } return x*f; } //**************************************** #define maxn 1000000+10 pair<pair<int ,int >,int > P[maxn]; int main() { int n=read(); int x,y; FOR(i,1,n) { x=read(); y=read(); P[i].first.first=x/1005;//注意 P[i].first.second=y; P[i].second=i; } sort(P+1,P+n+1); FOR(i,1,n) { cout<<P[i].second<<" "; } return 0; }
Codeforces Round #319 (Div. 1)C. Points on Plane 分块思想
原文：http://www.cnblogs.com/zxhl/p/4868313.html
