树状数组学习笔记

参考自:http://www.cnblogs.com/huangxincheng/archive/2012/12/05/2802858.html

0. 介绍(来自wikipedia)

　　- 树状数组, 又称二分索引树(Binary Indexed Tree, BIT), 用于高效计算数列的前缀和.

　　- 它可以以的时间得到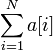，并同样以对某项加一个常数。

1. 数据结构定义

　　- 存放原始数据元素的数组a (i.e.  int[]  a)

　　- 树状数组 s   (i.e.   int[] s)

2. 说明:

　　- s 和 a 的大小一样大

　　- 下标从 1 开始计算, 因为后面要用到二进制格式末尾 连续0 的个数. 所以如果用 0 的话不太好处理.

3. 公式(2个等效的, 公式1用于理解, 计算主要用公式2)

　　- 1. s[i]=a[i-2^k+1]+a[i-2^k+1+1]+......+a[i-1]+a[i]   (if i-2^k+1 < i )   

　   - 2. s[i]=a[i] + s[j]   (j= i-1 decreasing to i-2^k+1 , j -= 2^t, t=lowbit(j) )

　　　  - s[i] 表示 树状数组第i个元素,  并不是前 i 个元素的和.

　　　　- k 表示 i 的二进制格式的末尾连续0的位数( i.e.    i=6₁₀=110₂   => k = 1) , 也代表s[i] 在树状结构中的层数 (i.e.  s[6] 在 level 1,  from level 0).

　　　　- 2^k 表示 s[i] 中包含原始数据 数组 a 中的元素个数  如s[6] = a[5] + a[6], 因为 k=1,  2^k为2, 利用公式计算得到 a[5] 和 a[6].  a[i-2^k+1] 算出 a[5]为起始项.

4. 工具代码

　　- 求 2^k  值

int lowbit(int x){
    return x & (-x);
}

　　- 建立树状数组

//根据原始数据数组建立树状数组 s
void build(){
    for (int i=1;i<=MAX_N;i++){ // s(i) 为计算的目标值
        s[i]=a[i]; // 基础值, s(i)必定包含 a(i)
        // 根据公式2, 倒着加回去, 从s(i-1) 加回去到 i-2k+1. 
        for (int j=i-1; j>=i-lowbit(i)+1;j-=lowbit(j)) //j每次减去的是j二进制中的每一位, 所以这个循环复杂度是O(logn)
            s[i]+=s[j];
    }
}

　　- 查询: 求前n项和, 继而也可以求任意区间之和. (logN)

//计算前n项和
int sumn (int n){
    int sum = 0;
    //利用公式进行计算.
    for (int i = n; i > 0; i -= lowbit(i)) 
        sum += s[i];
    return sum;
}

　　- 修改: 修改元素数据并同步更新树状数组的值.(logN)

//原始数组可以直接修改, 更新树状数组需要将包含 a[i]的所有元素更新.
// @param index: 修改的元素的下标. a[i]的修改对s[i]以前的元素没有影响.
// @param dalta : 修改量
void modify(int index, int delta){
    for (int j = index; j <= MAX_N; j += lowbit(j))
        s[j] += delta;
}

树状数组学习笔记

原文：http://www.cnblogs.com/roger9567/p/4866792.html