参考文献:
http://www.blogjava.net/zhenandaci/archive/2009/03/01/257237.html
http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html
NG的SVM课件
注意1:本文自然过渡并引出核函数的概念,比课件和其他教程上的说明更加让人理所当然地接受!
注意2:貌似对于SVM原问题求解,很多地方直接采用KKT条件求解。实际上,它也是通过求解对偶问题来得到KKT条件。如此,SVM原问题必须直接或者间接地经过对偶问题这一步的推导。
文中对核方法的表示K(x,z)其实x是常数,z是低维表示的,它和x同维,不要认为z是高维空间的变量,容易被一个例子:z=[z1,z2,z3]=[x,x2,x3]迷惑了双眼。参见NG的SVM中的14页。文中的下式也是如此:
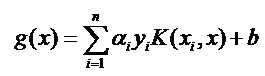
在对偶空间上说明这个问题。
(i)首先,我们在对偶空间中得到:
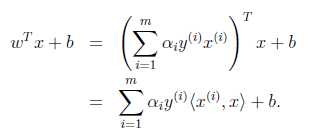
这里,我们假设x(i),y(i),x是d维向量。内积Rd×Rd->R
(ii)对于非线性问题,如果先找到一个映射Φ(x):Rd->R(d×d)使非线性问题变成线性问题(这里只是一个映射的特例),通常需要变到很高的维数空间去,问题变成了(未必是Rd->R(d×d),可能是Rd->R(d×c)):
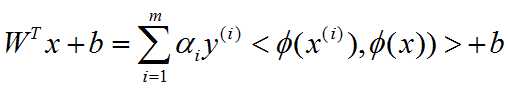 (1)
(1)
显然,算法复杂度的一个上界为:m×(d×d×2+d)+1,即O(m×d×d),注意到![]() 和
和![]() 的复杂度都为d×d,比如对于d=3时,x=[x1,x2,x3],其中的一种选择是:
的复杂度都为d×d,比如对于d=3时,x=[x1,x2,x3],其中的一种选择是:
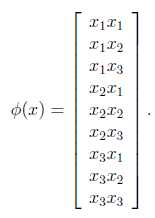
注意到![]() 是3×3=9维。
是3×3=9维。
(iii)对于上面的映射![]() 和
和![]() ,其中,
,其中,![]() 有
有
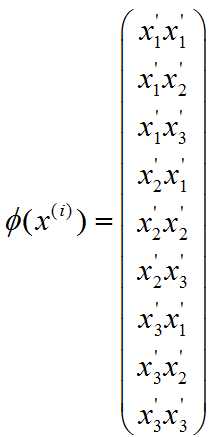 将
将![]() 和
和![]() 的表达式代入(1)中,得到:
的表达式代入(1)中,得到:
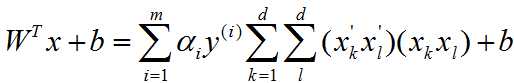
化简有:
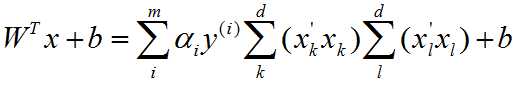
更进一步地,
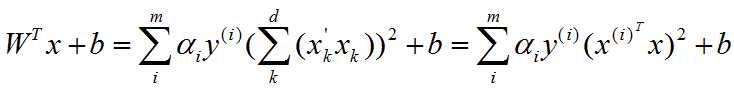
其中,令
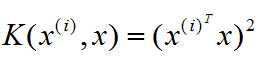
于是,
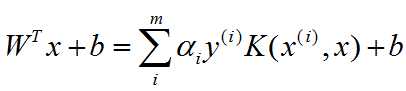
考虑到![]() 中,x和x(i)向量都是d维度,于是,总的计算复杂度为:m×(d+1)+1,即O(m×d)。
中,x和x(i)向量都是d维度,于是,总的计算复杂度为:m×(d+1)+1,即O(m×d)。
我们简化了两个工作:
(1)不用再去费劲去找![]()
(2)O(m×d×d)复杂度将到O(m×d)。如何只就![]() 这部分来说,O(d2)复杂度降到O(d)。这里不考虑矩阵相乘分成子矩阵以降低复杂度。只是一个上界的讨论。
这部分来说,O(d2)复杂度降到O(d)。这里不考虑矩阵相乘分成子矩阵以降低复杂度。只是一个上界的讨论。
既然有这两个如此强大的技巧,它被人们视为一种常用的东西,被称为核技巧,核函数,核方法。至于为啥叫这个奇葩的名字,我就不知道了。
附:
(1)这只是一种核函数,还有许许多多其它形式的。
(2)这里中的实际上除了支持向量之外的αm都为零。
(3)如果实在因为K(x,z)中的z纠结,那么不用管它,直接视为K好了。K为多项式核函数时,代入![]() 和
和![]() 时,由于对称性(也因为对称性K为半正定矩阵),总能化简成(xTz+c)这样简单的形式(或者是其它更一般的形式)。
时,由于对称性(也因为对称性K为半正定矩阵),总能化简成(xTz+c)这样简单的形式(或者是其它更一般的形式)。
原文:http://www.cnblogs.com/Wanggcong/p/4878141.html