通过计算每个训练数据到待分类元组的距离,取和待分类元组距离最近的K个训练数据,K个数据中哪个类别的训练数据占多数,则待分类元组就属于哪个类别。
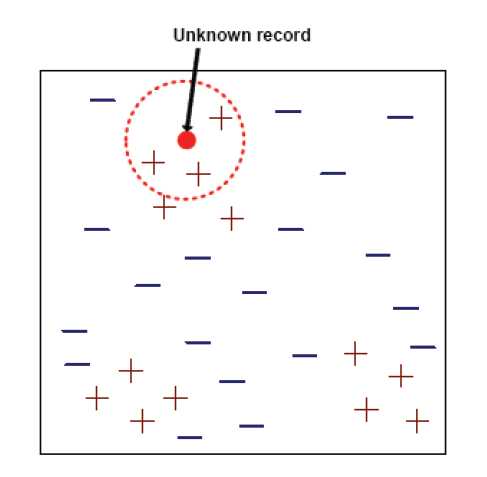
方法一:选出k个最近的邻居中的多数票的类标号
如果k过于小,那么将会对数据中存在的噪声过于敏感;
如果k过大,邻居中可能包含其他类的点;
一个经验的取值法则为k≤ ,q为训练元组的数目。商业算法通常以10作为默认值。
算法: K-近邻分类算法 输入: 训练数据T;近邻数目K;待分类的元组t。 输出: 输出类别c。 (1)N=?; // 定义近邻集 (2)FOR each d ∈T DO BEGIN (3) IF |N|≤K THEN // N的规模保持在k (4) N=N∪{d}; (5) ELSE (6) IF ?u∈N such that sim(t,u)<sim(t,d) THEN BEGIN /*如果N中存在数据u,使得t与u的相似度小于t与d的相似度(没有等于的情况保证了u!=d),即:新加入的d可以在N除去u之后加入到N中,d为N的新成员*/ (7) N=N-{u}; // 除去u (8) N=N∪{d}; // 加入d (9) END (10)END (11)c=class to which the most u∈N.
优点:原理简单,实现起来比较方便。支持增量学习。能对超多边形的复杂决策空间建模。
缺点:计算开销大,需要有效的存储技术和并行硬件的支撑。
原文:http://www.cnblogs.com/wanlong/p/4878954.html