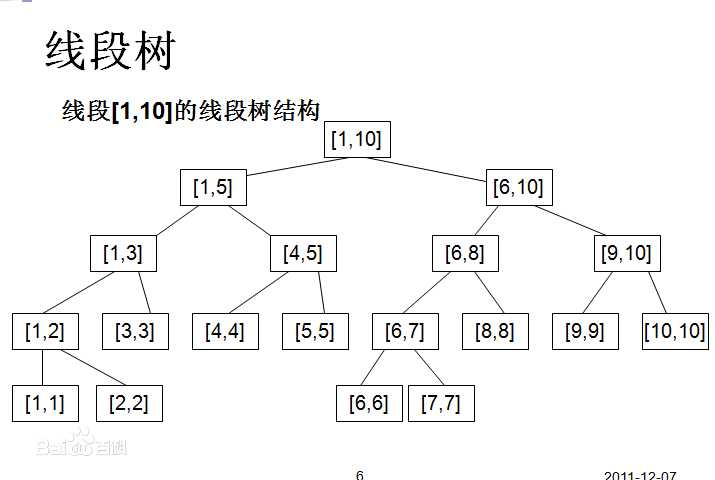
线段树是一棵完美二叉树,树上的每个节点都维护一个区间。根维护的是整个区间,每个节点维护的是父亲的区间二等分后的其中一个子区间。当有n个元素时,对区间的操作可以在O(logn)的时间内完成。
所以,线段树是擅长处理区间的!
从网上找了一个图:
RMQ(range minimum query)问题:
在给定数列a0,a1...an,给定s和t,线段树可以求as...at的最值,以求最小值为例,如下图:
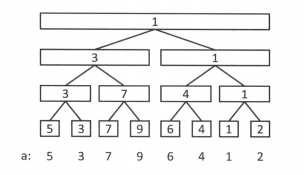
每个节点维护对应区间的最小值,例如根节点维护的是下标1到8的最小值,左子树维护的是1到4,右子书维护的是5到6,以此类推。
建树时,父节点取左右子节点的较小者。我比较喜欢用数组建树,因为非常简单清晰,下面是初始化线段树的代码:
1 #define max 999999999 2 int k,n,tree[10005];//n这里是数列里数字的个数 3 void init(){ 4 k=1;//k这里是树最后一层的叶子个数 5 while(k<n)//除第一层外,树的每一层都有2的n次方个节点,所以这里求的是k大于n的最小节点数 6 k<<=1;//输入的数字个数n可能小于最下面一层的叶子数 7 for(int i=1;i<=2*k-1;i++)//2*k-1是整个树节点的个数,全部设置为max,反正父节点取的是较小者 8 tree[i]=max; 9 }
n小于k时,树最后一层的其他值已经是max,所以不影响父节点,下面是线段树每插入一个值的更新:
1 void update(int pos,int val){//pos是树的下标,val是数的值 2 pos+=k-1;//这里数组下标是从1到n,树的下标也是从1到n,这就是叶子节点与数组下标的对应关系,大家可以画一画 3 tree[pos]=val; 4 while(k>1){ 5 pos/=2;//父节点 6 tree[pos]=tree[pos*2]<tree[pos*2+1]?tree[pos*2]:tree[pos*2+1]; 7 } 8 }
下面比较关键的是给定下标区间查找,我会在注释里说明:
1 //调用时query(输入a,输入b,1,l(英文l,不是数1),n) 2 int query(int a,int b,int pos,int l,int r){//a和b是想要查找的下标区间,l和r是当前节点维护的下标区间,pos是当前节点下标 3 if(a>r||b<l) 4 return max;//当想查找的区间完全超出当前节点维护的区间是,直接返回一个很大的数,反正是取最小 5 if(r-l==1){//这里很麻烦,有一种情况是,想查找的区间与维护的区间仅有一条边重合,例如想查找的是4、5,当前区间是5、6, 6 if(b==l)//这样,当到了当前区间左右差值为1时,不能向下继续了所以需要返回重合边所在的叶子的值(这里我尽量说明白,大家画一下会清楚很多) 7 return tree[2*pos]; 8 if(a==r) 9 return tree[2*pos+1]; 10 } 11 if(a<=l&&b>=r)//查找终结的条件就是想查找的区间大于节点维护的区间 12 return tree[pos]; 13 else{ 14 int vl=query(a,b,pos*2,l,(l+r)/2);//左节点 15 int vr=query(a,b,pos*2+1,(l+r)/2+1,r);//右节点 16 return vl<vr?vl:vr;//返回较小 17 } 18 }
OK,到这里,基本的算法就实现了,注意一下树的大小一定要合适。第一篇博客,有些地方想讲清楚可能讲的还不透彻,甚至里面会有错误,等我的理解更加深入之后,会继续修改的。
原文:http://www.cnblogs.com/zqy123/p/4899197.html