最小生成树

时间：2015-10-22 17:00:44 阅读：205 评论：0 收藏：0 [点我收藏+]

最小生成树

　　最小生成树就是将一个图中的若干边去掉，使之成为一棵树，这棵树的各条边的权值之和最小。

　　构造最小生成树有两个典型的算法——Prim算法和Kruskal算法。下面就分别介绍这两个算法。两个算法都是开始将各个顶点孤立，然后依次选取若干边将顶点连接起来构成一棵树。

Prim算法

　　算法的流程大致如下：

（1）选取任意顶点V_{0，将其放入已访问集合V（未访问集合为U）。}

（2）遍历已访问集合中所有顶点，选取到未访问集合中的顶点距离最小的点加入访问集合。

（3）当所有的顶点都在已访问集合中时，算法结束。

因此，我们定义lowcost数组记录V到U中的i顶点中的距离，定义closeset数组记录i顶点是由哪一个顶点延伸出来的。以此来构造最后的生成树。

 1 #include<cstdio>
 2 #define MAXSZIE 100
 3 typedef struct Vertex
 4 {
 5     int num;
 6 } Vertex;
 7 typedef struct MGraph
 8 {
 9     int n,e;
10     int edges[MAXSZIE][MAXSZIE];
11     Vertex vex[MAXSZIE];
12 } MGraph;
13 int BTree[MAXSZIE][MAXSZIE];
14 MGraph create()
15 {
16     int n,e;
17     int a,b,val;
18     MGraph g;
19     scanf("%d%d",&n,&e);
20     g.n=n;
21     g.e=e;
22     for(int i=0; i<n; i++)
23         g.vex[i].num=i;
24     for(int i=0; i<e; i++)
25         for(int j=0; j<e; j++)
26             g.edges[i][j]=99999;
27     for(int i=0; i<e; i++)
28     {
29         scanf("%d%d%d",&a,&b,&val);
30         g.edges[a][b]=val;
31         g.edges[b][a]=val;
32     }
33     return g;
34 }
35 void prim(MGraph g,int v0)
36 {
37     int closeset[MAXSZIE];
38     int lowcost[MAXSZIE];   //生成树到其余节点权值
39     int father[MAXSZIE];
40     int bset[MAXSZIE];
41     for(int i=0; i<g.n; i++)
42     {
43         bset[i]=0;
44         closeset[i]=0;
45         lowcost[i]=g.edges[v0][i];
46     }
47     bset[v0]=1;
48     for(int i=1; i<g.n; ++i)
49     {
50         int minval=9999;
51         int k;
52         for(int j=1; j<g.n; ++j)
53         {
54             if(bset[j]==0&&lowcost[j]<=minval)
55             {
56                 minval=lowcost[j];
57                 k=j;
58             }
59         }
60         father[k]=closeset[k];
61         BTree[k][father[k]]=minval;
62         BTree[father[k]][k]=minval;
63         bset[k]=1;
64         for(int j=1; j<g.n; ++j)
65         {
66             if(bset[j]==0&&g.edges[k][j]<lowcost[j])
67             {
68                 lowcost[j]=g.edges[k][j];
69                 closeset[j]=k;
70             }
71 
72         }
73     }
74 }
75 int main()
76 {
77     MGraph g = create();
78     prim(g,0);
79     for(int i=0; i<g.n; i++)
80     {
81         for(int j=0; j<g.n; j++)
82             printf("%d\t",BTree[i][j]);
83         printf("\n");
84     }
85     return 0;
86 }

　　如上述代码所示，我们使用邻接矩阵表示图，不连通的顶点之前的权值为无穷大。

　　依次看所有的节点，每次选取最小的边进行扩展，所以就是每次选择一个顶点加入到最小生成树中，当我们将所有顶点遍历一遍（最外层循环）的时候，算法结束。

　　每次扩展节点，我们选取到未扩展集合权值最小的边，也就是选取lowcost中值最小的，记录其顶点坐标k。延伸出k的closeset的值就是k的父节点。

　　每扩展完一次，就要对lowcost数组和closeset数组进行更新，对应代码的66~70行，也就是说，如果新延伸的节点k到未访问集合的距离如果更短，那么未访问集合中下一个延伸的节点肯定是由k延伸出去的，否则是由其他点延伸出去的。这个显然啊，因为下一次也是从V的邻接边中找最小的，你从k出发，到未访问的节点小于你之前的lowcost数组中的值，那么下一次延伸的节点必然是从k出去的（从其他节点到未访问集合的距离已经被更新）。

　　说的有点乱，举个栗子。

　　　　　　　　　　　　　　　　　　　　　　　　技术分享

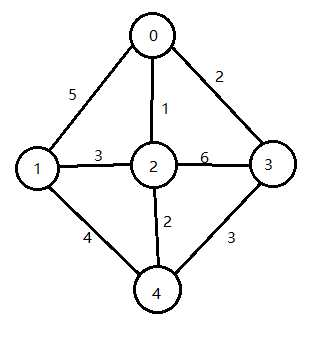
　　一开始，我们将0标记为已访问。所有的节点一开始默认从0延伸出去。此时，lowcost[1]=5，下一次，找到了2节点（就是上边所说的k），2加入到集合中，此时，从2到1的距离为3，比lowcost[1]=5要小，所以，1肯定不能由0延伸出去，肯能是从2延伸，那么就要更新1的lowcost值和closeset值，当我们扩展1的时候，2通过closeset就直接找到了其父节点。

　　对于Prim算法的时间复杂度，很明显是O（n²）的。

Kruskal算法

　　算法的大致流程如下：

（1）将所有的边按从小到大排序。

（2）从小到大依次选择边构成树，注意不能成环。

（3）所有的边遍历一遍后，算法结束

将节点依次加入集合中构成树，需要用到并查集。

  1 #include<cstdio>
  2 #define MAXSZIE 100
  3 typedef struct Vertex
  4 {
  5     int num;
  6 } Vertex;
  7 typedef struct MGraph
  8 {
  9     int n,e;
 10     int edges[MAXSZIE][MAXSZIE];
 11     Vertex vex[MAXSZIE];
 12 } MGraph;
 13 int BTree[MAXSZIE][MAXSZIE];
 14 typedef struct Road
 15 {
 16     int a,b;
 17     int weight;
 18 } Road;
 19 Road r[MAXSZIE];
 20 int count=0;
 21 MGraph create()
 22 {
 23 
 24     int n,e;
 25     int a,b,val;
 26     MGraph g;
 27     scanf("%d%d",&n,&e);
 28     g.n=n;
 29     g.e=e;
 30     for(int i=0; i<n; i++)
 31         g.vex[i].num=i;
 32     for(int i=0; i<e; i++)
 33         for(int j=0; j<e; j++)
 34             g.edges[i][j]=99999;
 35     for(int i=0; i<e; i++)
 36     {
 37         scanf("%d%d%d",&a,&b,&val);
 38         g.edges[a][b]=val;
 39         g.edges[b][a]=val;
 40         r[count].a=a;
 41         r[count].b=b;
 42         r[count].weight=val;
 43         count++;
 44     }
 45     return g;
 46 }
 47 int father[MAXSZIE];
 48 void init(MGraph g)
 49 {
 50     for(int i=0; i<g.n; ++i)
 51         father[i]=i;
 52 }
 53 int getfather(int x)
 54 {
 55     if(x!=father[x])
 56         father[x]=getfather(father[x]);
 57     return father[x];
 58 }
 59 void unio(int x,int y)
 60 {
 61     int m,n;
 62     m=getfather(x);
 63     n=getfather(y);
 64     if(m!=n)
 65     {
 66         father[m]=n;
 67         BTree[x][y]=1;
 68     }
 69 }
 70 void getSort(MGraph g)
 71 {
 72     Road tempr;
 73     for(int i=0; i<g.e-1; ++i)
 74     {
 75         for(int j=i+1; j<g.e; ++j)
 76         {
 77             if(r[i].weight>r[j].weight)
 78             {
 79                 tempr=r[j];
 80                 r[j]=r[i];
 81                 r[i]=tempr;
 82             }
 83         }
 84     }
 85 }
 86 void Kruskal(MGraph g)
 87 {
 88     getSort(g);
 89     int x,y;
 90     for(int i=0; i<g.e; i++)
 91     {
 92         unio(r[i].a,r[i].b);
 93     }
 94 }
 95 int main()
 96 {
 97     MGraph g = create();
 98     init(g);
 99     Kruskal(g);
100     for(int i=0; i<g.n; ++i)
101     {
102         for(int j=0; j<g.n; ++j)
103         {
104             printf("%d\t",BTree[i][j]);
105         }
106         printf("\n");
107     }
108     return 0;
109 }

　　算法很简单，只要对边进行排序，然后依次合并就可以了，这里就不举栗子了。所以算法的时间复杂度与排序算法的时间复杂度相同。

最小生成树

原文：http://www.cnblogs.com/wktwj/p/4901519.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)