设计不同的结点结构可构成不同形式的链式储存结构。由二叉树的结点由一个数据元素和分别指向其左、右子树的两个分支构成,则表示二叉树的链表中的结点至少包含三个域:数据域和左、右指针域
一下是二叉链表的定义和部分基本操作的函数原型说明:
#ifndef BINARY_LINKED_LIST_TREE_H #define BINARY_LINKED_LIST_TREE_H //---------二叉树的二叉链表储存表示----------- #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define MYOVERFLOW -2 typedef int Status; typedef char TElemType; typedef struct BiTNode { TElemType data; BiTNode *lchild, *rchild; }*BiTree; //------------基本操作的函数原型说明(部分)------------ Status CreateBiTree(BiTree &T); //T表示这个树的根节点的指针 //按先序次序输入二叉树中结点的值(一个字符),空格字符表示空树, //构造二叉链表表示的二叉树T Status VisitBiTree(BiTree); //输出结点的数据域 Status PreOrderTraverse(BiTree T, Status(*Visit)(BiTree)); //T表示这个树的根节点的指针 //采用二叉链表储存结构,Visit是对结点操作的对应函数 //先序遍历二叉树T,对每个结点调用函数Visit一次且仅一次。 //一旦visit()失败,则操作失败 Status InOrderTraverse(BiTree T, Status(*Visit)(BiTree)); //T表示这个树的根节点的指针 //采用二叉链表储存结构,Visit是对结点操作的对应函数 //中序遍历二叉树T,对每个结点调用函数Visit一次且仅一次。 //一旦visit()失败,则操作失败 Status InOrderTraverse_2(BiTree T, Status(*Visit)(BiTree)); //采用二叉链表储存结构,Visit是对数据元素操作的应用函数。 //中序遍历二叉树T的非递归算法,对每个数据元素调用函数Visit Status InOrderTraverse_3(BiTree T, Status(*Visit)(BiTree)); //采用二叉链表储存结构,Visit是对数据元素操作的应用函数。 //中序遍历二叉树T的非递归算法,对每个数据元素调用函数Visit Status PostOrderTraverse(BiTree T, Status(*Visit)(BiTree)); //T表示这个树的根节点的指针 //采用二叉链表储存结构,Visit是对结点操作的对应函数 //后序遍历二叉树T,对每个结点调用函数Visit一次且仅一次。 //一旦visit()失败,则操作失败 Status LevelOrderTraverse(BiTree T, Status(*Visit)(BiTree)); //T表示这个树的根节点的指针 //采用二叉链表储存结构,Visit是对结点操作的对应函数 //层序遍历二叉树T,对每个结点调用函数Visit一次且仅一次。 //一旦visit()失败,则操作失败
Status Destroy(BiTree T);//摧毁T这个节点
Status DestroyBiTree(BiTree &T);
//摧毁二叉树T
#endif
在二叉树的一些应用中,常常要求在树中查找具有某种特征的结点,或者对树中全部结点逐一进行某种处理。这就提出了一个遍历二叉树的问题,即如何按某条搜索路径寻访树中每个结点,使得每个结点均被访问一次,而且仅被访问一次。二叉树的遍历又有很多情况,其中先序、中序、后序、层序遍历是常见的情况
上述操作的实现:
#include"stdafx.h" #include"ADT.h" #include<deque> #include<stack> //------------基本操作的函数原型说明(部分)------------ Status CreateBiTree(BiTree &T) //T表示这个树的根节点的指针 //按先序次序输入二叉树中结点的值(一个字符),字符为空表示空树, //构造二叉链表表示的二叉树T { char ch; ch = getchar(); if (ch == ‘ ‘){ T = NULL; return OK; } else { if (!(T = (BiTNode *)malloc(sizeof(BiTNode))))exit(MYOVERFLOW); T->data = ch; CreateBiTree(T->lchild); CreateBiTree(T->rchild); } return OK; } Status VisitBiTree(BiTree T) //输出结点的数据域 { cout << T->data << " "; return OK; } Status Destroy(BiTree T){//摧毁T这个节点 if (T){ free(T); } return OK; } Status PreOrderTraverse(BiTree T, Status(*Visit)(BiTree)) //T表示这个树的根节点的指针 //采用二叉链表储存结构,Visit是对结点操作的对应函数 //先序遍历二叉树T,对每个结点调用函数Visit一次且仅一次。 //一旦visit()失败,则操作失败 { if (T){ BiTree lchild = T->lchild, rchild = T->rchild; if(Visit(T)) if (PreOrderTraverse(lchild,Visit)) if (PreOrderTraverse(rchild, Visit))return OK; return ERROR; } return OK; } Status InOrderTraverse(BiTree T, Status(*Visit)(BiTree)) //T表示这个树的根节点的指针 //采用二叉链表储存结构,Visit是对结点操作的对应函数 //中序遍历二叉树T,对每个结点调用函数Visit一次且仅一次。 //一旦visit()失败,则操作失败 { if (T){ BiTree lchild = T->lchild, rchild = T->rchild; if (InOrderTraverse(lchild, Visit)) if (Visit(T)) if (InOrderTraverse(rchild, Visit))return OK; return ERROR; } return OK; } Status InOrderTraverse_2(BiTree T, Status(*Visit)(BiTree)) //采用二叉链表储存结构,Visit是对数据元素操作的应用函数。 //中序遍历二叉树T的非递归算法,对每个数据元素调用函数Visit { stack<BiTree> sta; sta.push(T); BiTree p; while (!sta.empty()){ while (p = sta.top())sta.push(p->lchild); sta.pop(); if (!sta.empty()){ p = sta.top(); sta.pop(); if (!Visit(p))return ERROR; sta.push(p->rchild); } } return OK; } Status InOrderTraverse_3(BiTree T, Status(*Visit)(BiTree)) //采用二叉链表储存结构,Visit是对数据元素操作的应用函数。 //中序遍历二叉树T的非递归算法,对每个数据元素调用函数Visit { stack<BiTree> sta; BiTree p = T; while (p || !sta.empty()){ if (p){ sta.push(p); p = p->lchild; } else{ p = sta.top(); sta.pop(); if (!Visit(p))return ERROR; p = p->rchild; } } return OK; } Status PostOrderTraverse(BiTree T, Status(*Visit)(BiTree)) //T表示这个树的根节点的指针 //采用二叉链表储存结构,Visit是对结点操作的对应函数 //后序遍历二叉树T,对每个结点调用函数Visit一次且仅一次。 //一旦visit()失败,则操作失败 { if (T){ BiTree lchild = T->lchild, rchild = T->rchild; if (PostOrderTraverse(lchild, Visit)) if (PostOrderTraverse(rchild, Visit)) if (Visit(T))return OK; return ERROR; } return OK; } Status LevelOrderTraverse(BiTree T, Status(*Visit)(BiTree)) //T表示这个树的根节点的指针 //采用二叉链表储存结构,Visit是对结点操作的对应函数 //层序遍历二叉树T,对每个结点调用函数Visit一次且仅一次。 //一旦visit()失败,则操作失败 { deque<BiTree> deq; if (T){ deq.push_back(T); while (!deq.empty()){ auto temp = deq.at(0); Visit(temp); if (temp->lchild) deq.push_back(temp->lchild); if (temp->rchild) deq.push_back(temp->rchild); deq.pop_front(); } } cout << endl; return OK; } Status DestroyBiTree(BiTree &T) //摧毁二叉树T { if (PreOrderTraverse(T, Destroy))return OK; return FALSE; }
主函数:
// 二叉链表.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" int _tmain(int argc, _TCHAR* argv[]) { BiTree T; cout << "中序输入二叉树,如果某个节点的左右子树为空,则输入两个空格:" << endl; CreateBiTree(T); cout << "先序遍历" << endl; PreOrderTraverse(T, VisitBiTree); cout << endl; cout << "中序遍历"<<endl; InOrderTraverse(T, VisitBiTree); cout << endl; InOrderTraverse_2(T, VisitBiTree); cout << endl; InOrderTraverse_3(T, VisitBiTree); cout << endl; cout << "后序遍历"<<endl; PostOrderTraverse(T, VisitBiTree); cout << endl; cout << "层序遍历"<<endl; LevelOrderTraverse(T, VisitBiTree); DestroyBiTree(T); return 0; }
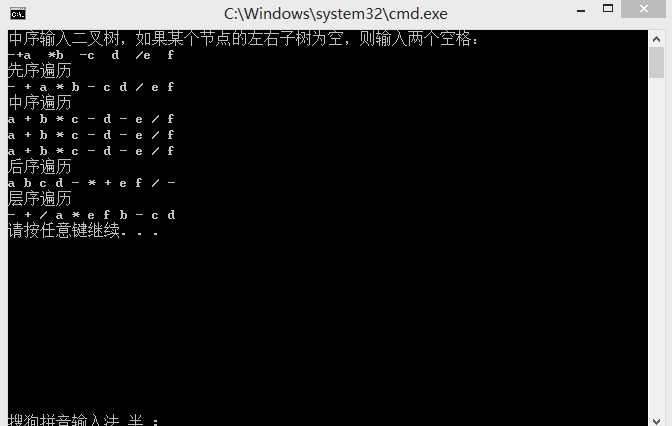
结果:(在vs2013中实现,注意要在stadfx.h中包含相应的头文件)
原文:http://www.cnblogs.com/csudanli/p/4908118.html