There is a tower defense game with n levels(missions). The n levels form a tree whose root is level 1.
In the i-th level, you have to spend pi units of money buying towers and after the level, you can sell the towers so that you have qi units of money back.
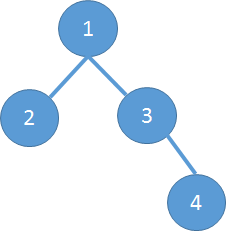
Each level is played once. You can choose any order to complete all the levels, but the order should follow the following rules:
1: A level can be played when all its ancestors are completed.
2: The levels which form a subtree of the original tree should be completed consecutively in your order.
You want to know in which order of completion you can bring the minimum money before starting the first level.
The first line contains one single integers, n - the number of levels. (1<=n<=10000)
The next n lines describes the levels. Each line contains 2 integers, pi and qi which are described in the statement. (0<=qi<=pi<=20000)
The next n-1 lines describes the tree. Each line contains 2 integers, ai and bi which means there is an edge between level ai and level bi.
For 30% of the data, n<=100.
For 60% of the data, n<=1000.
Print one line with an single integer representing the minimum cost.
There are two orders of completing all levels which are: 1234 and 1342.
In the order 1234, the minimum beginning money is 5.
In the order 1342, the minimum beginning money is 7.
1324 is not a valid order because level 3 and level 4 are not completed consecutively.
Sample Input
4 2 1 4 3 2 1 2 1 1 2 1 3 3 4
Sample Output
5
Solution:
1 #include <cstdio> 2 #include <algorithm> 3 #include <vector> 4 #include <cstring> 5 using namespace std; 6 7 #define max(a,b) (a>b?a:b) 8 9 10 #define MAXN 10010 11 int p[MAXN]; 12 int q[MAXN]; 13 vector<int> edges[MAXN]; 14 15 void addEdge(int u, int v) { 16 edges[u].push_back(v); 17 edges[v].push_back(u); 18 } 19 20 int in[MAXN]; 21 int out[MAXN]; 22 int vis[MAXN] = { 0 }; 23 24 struct unit { 25 int input; 26 int output; 27 }; 28 29 int dfs(int u, int *vis) { 30 vis[u] = 1; 31 if (in[u] >= 0) { 32 return in[u]; 33 } 34 35 vector<unit> ch; 36 for (int i = 0; i < edges[u].size(); ++i) { 37 int v = edges[u][i]; 38 if (!vis[v]) { 39 dfs(v, vis); 40 ch.push_back({ in[v], out[v] }); 41 } 42 } 43 if (ch.size() == 0) { 44 out[u] = q[u]; 45 return in[u] = p[u]; 46 } 47 48 sort(ch.begin(), ch.end(), [](const unit &u1, const unit &u2) { 49 return max(u1.input, u2.input + u1.input - u1.output) < max(u2.input, u1.input + u2.input - u2.output); 50 }); 51 52 int a = ch.back().input; 53 int d = ch.back().input - ch.back().output; 54 for (int i = ch.size() - 2; i >= 0; --i) { 55 a = max(ch[i].input, ch[i].input - ch[i].output + a); 56 d += ch[i].input - ch[i].output; 57 } 58 59 60 in[u] = max(p[u], a + p[u] - q[u]); 61 out[u] = in[u] - d - (p[u] - q[u]); 62 return in[u]; 63 } 64 65 int main() { 66 int N; 67 scanf("%d", &N); 68 for (int i = 1; i <= N; ++i) { 69 scanf("%d %d", p + i, q + i); 70 } 71 for (int i = 0; i < N - 1; ++i) { 72 int u, v; 73 scanf("%d %d", &u, &v); 74 addEdge(u, v); 75 } 76 memset(in, -1, sizeof in); 77 printf("%d\n", dfs(1,vis)); 78 }
hihoCoder #1199 Tower Defense Game
原文:http://www.cnblogs.com/liew/p/4915765.html