主题模型(topic modeling)是一种常见的机器学习应用,主要用于对文本进行分类。传统的文本分类器,例如贝叶斯、KNN和SVM分类器,只能将测试对象分到某一个类别中,假设我给出三个分类:“算法”、“网络”和“编译”让其判断,这些分类器往往将对象归到某一类中。
但是如果一个外行完全给不出备选类别,有没有分类器能够自动给出类别判断呢?
有,这样的分类器就是主题模型。
潜在狄立克雷分配(Latent Dirichlet Allocation,LDA)主题模型是最简单的主题模型,它描述的是一篇文章是如何产生的。其原理如下图所示:
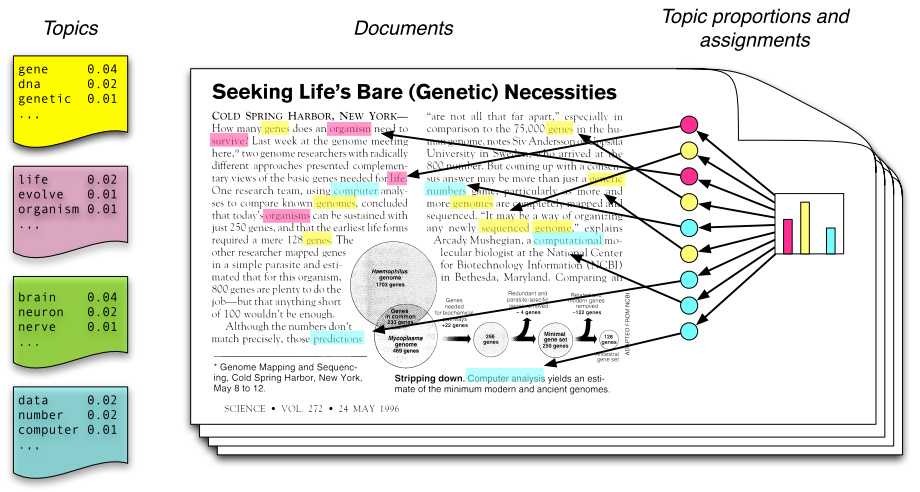
从左往右看,一个主题是由一些词语的分布定义的,比如蓝色主题是由2%几率的data,2%的number……构成的。一篇文章则是由一些主题构成的,比如右边的直方图。具体产生过程是,从主题集合中按概率分布选取一些主题,从该主题中按概率分布选取一些词语,这些词语构成了最终的文档(LDA模型中,词语的无序集合构成文档,也就是说词语的顺序没有关系)。
如果我们能将上述两个概率分布计算清楚,那么我们就得到了一个模型,该模型可以根据某篇文档推断出它的主题分布,即分类。由文档推断主题是文档生成过程的逆过程。
在《LDA数学八卦》一文中,对文档的生成过程有个很形象的描述:

LDA是一种使用联合分布来计算在给定观测变量下隐藏变量的条件分布(后验分布)的概率模型,观测变量为词的集合,隐藏变量为主题。
LDA的生成过程对应的观测变量和隐藏变量的联合分布如下:
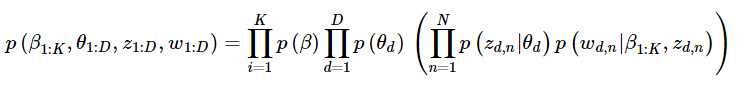
式子的基本符号约定——β表示主题,θ表示主题的概率,z表示特定文档或词语的主题,w为词语。
β1:K为全体主题集合,其中βk是第k个主题的词的分布(如图1左部所示)。第d个文档中该主题所占的比例为θd,其中θd,k表示第k个主题在第d个文档中的比例(图1右部的直方图)。第d个文档的主题全体为zd,其中zd,n是第d个文档中第n个词的主题(如图1中有颜色的圆圈)。第d个文档中所有词记为wd,其中wd,n是第d个文档中第n个词,每个词都是固定的词汇表中的元素。
p(β)表示从主题集合中选取了一个特定主题,p(θd)表示该主题在特定文档中的概率,大括号的前半部分是该主题确定时该文档第n个词的主题,后半部分是该文档第n个词的主题与该词的联合分布。连乘符号描述了随机变量的依赖性,用概率图模型表述如下:
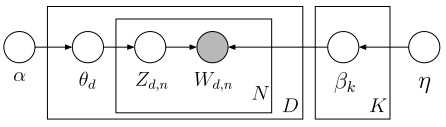
比如,先选取了主题,才能从主题里选词。具体说来,一个词受两个随机变量的影响(直接或间接),一个是确定了主题后文档中该主题的分布θd,另一种是第k个主题的词的分布βk(也就是图2中的第二个坛子)。
沿用相同的符号,LDA后验分布计算公式如下:
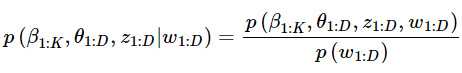
分子是一个联合分布,给定语料库就可以轻松统计出来。但分母无法暴力计算,因为文档集合词库达到百万(假设有w个词语),每个词要计算每一种可能的观测的组合(假设有n种组合)的概率然后累加得到先验概率,所以需要一种近似算法。
基于采样的算法通过收集后验分布的样本,以样本的分布求得后验分布的近似。
θd的概率服从Dirichlet分布,zd,n的分布服从multinomial分布,两个分布共轭,所谓共轭,指的就是先验分布和后验分布的形式相同:
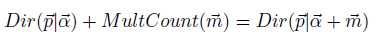
两个分布其实是向量的分布,向量通过这两个分布取样得到。采样方法通过收集这两个分布的样本,以样本的分布近似。
开源项目:
A Java implemention of LDA
LDA4j:https://github.com/hankcs/LDA4j
原地址:http://www.hankcs.com/nlp/lda-java-introduction-and-implementation.html
原文:http://www.cnblogs.com/zqliu133/p/4918446.html