本系列从零起步，作为学习笔记与大家分享，从基础的数学和图形理论，一步一步实现基于物理的渲染。

由于光源是三维空间中的辐射光能，对于其传播范围通常使用立体角来描述，先来看一下什么是立体角。

立体角

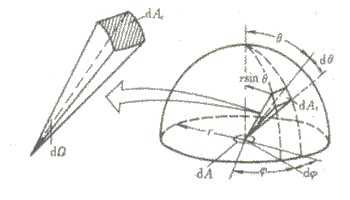
立体角表示一个锥面所围成的空间部分，用符号ω表示。

立体角是以圆锥体的顶点为心，半径为r的球面被锥面所截得的面积来度量的，度量单位为“球面度”（steradian，符号∶sr）。球面度表示为三维弧度。

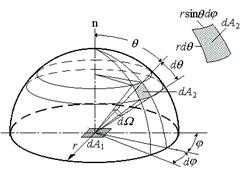
在球坐标系中，球面的极小面积A₂为：

\({dA}_{2}=({r}\,\sin\theta\, {d}\varphi )({r\,d\theta })={r}^{2}(\sin\theta\,{d\theta }\,{d}\varphi)\)

整个球面面积为\({dA}\)的积分： 

\({A}=\int {dA}_{2}=\int_{0}^{2\pi}\int_{0}^{\pi}({r}\,\sin\theta\, {d}\varphi*{r\,d\theta })={r}^{2}\int_{0}^{2\pi}{d}\varphi\int_{0}^{\pi}\sin\theta\,{d}\theta\)

（未完待续）

PBR Step by Step（一）立体角

原文：http://www.cnblogs.com/jerrycg/p/4924761.html