数学猜想并不总是对的,错误的数学猜想不占少数。只不过因为反例太大,找出反例实在是太困难了。这篇日志收集了很多“大反例”的例子,里面提到的规律看上去非常诱人,要试到相当大的数时才会出现第一个反例。
千万不要迷信规律
圆上有 n 个点,两两之间连线后,最多可以把整个圆分成多少块?
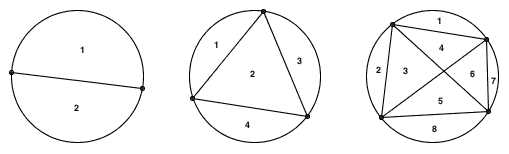
上图显示的就是 n 分别为 2 、 3 、 4 的情况。可以看到,圆分别被划分成了 2 块、 4 块、 8 块。规律似乎非常明显:圆周上每多一个点,划分出来的区域数就会翻一倍。
事实上真的是这样吗?让我们看看当 n = 5 时的情况:
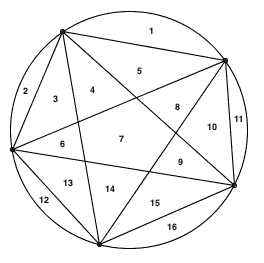
果然不出所料,整个圆被分成了 16 块,区域数依旧满足 2n-1 的规律。此时,大家都会觉得证据已经充分,不必继续往下验证了吧。偏偏就在 n = 6 时,意外出现了:
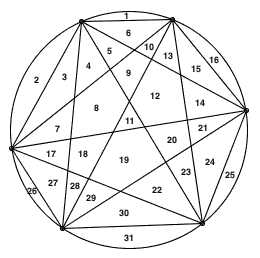
此时区域数只有 31 个。
最有名的素数生成公式
1772 年,Euler 曾经发现,当 n 是正整数时, n2 + n + 41 似乎总是素数。事实上,n 从 1 一直取到 39,算出来的结果分别是:
43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281,
313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853,
911, 971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601
这些数全都是素数。第一次例外发生在 n = 40 的时候,此时 402 + 40 + 41 = 402 + 40 + 40 + 1 = (40 + 1)(40 + 1) = 41 × 41。
xn - 1 的因式分解
x2 - 1 分解因式后等于 (x + 1)(x - 1) 。 x20 - 1 分解因式后等于
(x - 1) (x + 1) (x2 + 1) (x4 - x3 + x2 - x + 1) (x4 + x3 + x2 + x + 1) (x8 - x6 + x4 - x2 + 1)
对于所有的正整数 n , xn - 1 因式分解后各项系数都只有可能是 1 或者 -1 吗?据说有人曾经算到了 x100 - 1 ,均没有发现反例,终于放心大胆地做出了这个猜想。悲剧的是,这个猜想是错误的,第一个反例出现在 n = 105 的情况, x105 - 1 分解出来等于
(x - 1) (x2 + x + 1) (x4 + x3 + x2 + x + 1) (x6 + x5 + x4 + x3 + x2 + x + 1)
(x8 - x7 + x5 - x4 + x3 - x + 1) (x12 - x11 + x9 - x8 + x6 - x4 + x3 - x + 1)
(x24 - x23 + x19 - x18 + x17 - x16 + x14 - x13 + x12 - x11 + x10 - x8 + x7 - x6 + x5 - x + 1)
(x48 + x47 + x46 - x43 - x42 - 2 x41 - x40 - x39 + x36 + x35 + x34 + x33 + x32 + x31 - x28
- x26 - x24 - x22 - x20 + x17 + x16 + x15 + x14 + x13 + x12 - x9 - x8 - 2 x7 - x6 - x5 + x2 + x + 1)
以 2 为底的伪素数
下面是当 n 较小的时候, n 与 2n - 2 的值。

似乎有这样的规律: n 能整除 2n - 2 ,当且仅当 n 是一个素数。如果真是这样的话,我们无疑有了一种超级高效的素数判定算法( 2n 可以用二分法速算,期间可以不断模 n )。国外数学界一直传有“中国人 2000 多年前就发现了这一规律”的说法,后来发现其实是对《九章算术》一书的错误翻译造成的。再后来人们发现,这个规律竟然是错误的。第一个反例是 n = 341,此时 341 能够整除 2341 - 2 ,但 341 = 11 × 31 。
事实上,根据 Fermat 小定理,如果 p 是素数,那么 p 一定能整除 2n - 2。不过,它的逆定理却是不成立的,上面提到的 341 便是一例。我们把这种数叫做以 2 为底的伪素数。由于这种素数判定法的反例出人意料的少,我们完全可以用它来做一个概率型的素数判定算法。事实上,著名的Miller-Rabin 素性测试算法就是用的这个原理。
Perrin 伪素数
定义 f(n) = f(n - 2) + f(n - 3) ,其中 f(1) = 0 , f(2) = 2 , f(3) = 3 。这个数列叫做 Perrin 数列。
原文:http://www.cnblogs.com/abapscript/p/4925342.html