题意:给n个点,以这n个点为圆心画圆,使得所有的圆与其相邻的圆相切。
求n个圆最小的面积和。
分析:很容易想到确定了其中一个圆的半径之后,其他的圆的半径也能随之确定了。
画一画三个点的和四个点的,会发现有区别。
三个点的你会发现你稍微画次一点就不能满足 与相邻的都相切的条件了
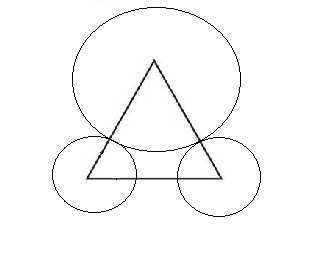
而四个点的,很轻易就能画出来
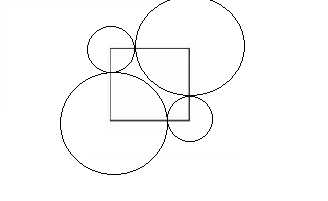
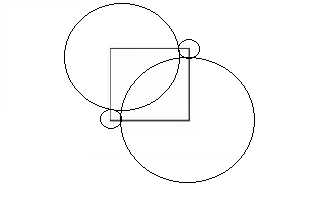
所以可以分成两类:奇数个点的 和 偶数个点的
奇数个点的因为答案唯一,因此直接$\frac{R}{2}$就行了
至于偶数个的
因为圆的半径和面积是成单峰函数的。因此可以对半径三分来求解。
其中 过程中r是不能出现负数的
如果解出的区间的右端点要小于左端点,那就是impossible了
原文:http://www.cnblogs.com/Empress/p/4928731.html