独立集与点覆盖

As it is shown in the fig, we have a graph G(V, E).

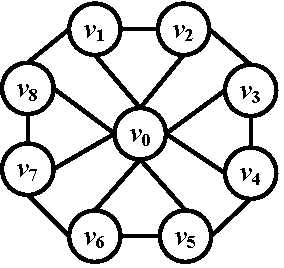
1. Inpdependent Set:  A set of nodes S\( \subset \)V is independent if no pair of nodes from S is connected by an edge.

     Eg. {\(v_0\)}, {\(v_1, v_4, v_7\)}, {\(v_1, v_3, v_4, v_7\)} 

2. Vertex Cover: A set of nodes S\(\subset\)V is a vertex cover if every edge e\(\in\)E has at least one end in S.

     Eg. {\(v_0, v_1, v_3, v_5, v_7\)}, {\(v_1, v_2, v_3, v_4, v_5, v_6, v_7, v_8\)} 

Theorem: Let G(V, E) be a graph. Then S is an independent set iff its complement V-S is a vertex cover.

Proof: Let S be an independent set, consider an arbitrary edge e\(\in\)E, where e=(u, v), since S is independent, it can not be the case that both u and v are in S. So, at least one of u or v must be in V-S. Thus, V-S must be vertex cover. Conversely, suppose V-S is a vertex cover, consider any pair of vertex u, v in S, if they are joined by an edge e, then neither end of e would be in V-S, a contrandiction.  Thus, S must be an independent set.

独立集与点覆盖

原文：http://www.cnblogs.com/pengwu/p/4932528.html