由于大二下学期我们专业才上《数据结构》，所以我先找到了一个学堂在线的DSA(Date Structures and Algorithms)公开课，想系统地学习一下数据结构，看到栈这一节感觉有挺多可以做笔记的地方，也有很多有用的东西，因此就写在Blog里面分享一下。
栈
简介：栈（stack）又名堆栈，它是一种线性表。其特点在于仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。向一 个栈插入新元素又称作进栈(入栈 or 压栈)；从一个栈删除元素又称作出栈(退栈)。
其重要的特性可以简述为LIFO(Last In First Out),也就是“后入先出”，类似于在桶中放盘子，只能从顶部放上去，也只能从最高处拿出去。
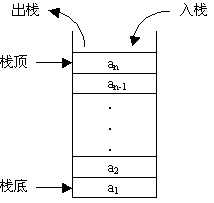
如下图，我们可以用一种序列来表示这个栈[a1,a2...an-1,an>,其中尖括号>表示栈顶，中括号[表示栈底。
对于栈的应用可以归纳如下图：
栈混洗：
简介：将栈中元素按照一定次序重新排序(类似洗牌)。这将需要新加入两个栈，其中一个栈(A)作为中介将原栈(O)的元素按一定顺序压入另一个栈(B)中。
图示如下:
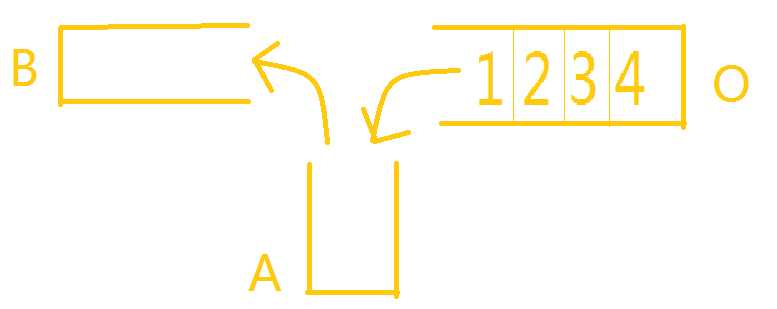
栈混洗并不能对栈O中的元素进行全排，因此我们可能需要甄别怎样的序列不能经过栈混洗得到。首先我们来讨论一下栈混洗可以得到的序列数量。
栈混洗可以得到的序列数量
设若有n个元素，对第一个元素1进行分析，若1压入栈A后直接压入栈B，那么A将成为空栈，后续n-1个元素此时将要入栈的情况和n个元素入栈的情况相同，只是规模减少了一个元素。那么在压栈出栈过程中，对任一个使栈A空栈的第k个元素，此时在栈B中有k个元素，在栈O中有n-k个元素，此时和n个元素的时候入栈情况相同，只是规模减少了k个元素。
由此我们可以得到一段分而治之的递推式(设对n个元素的栈有X(n)种混洗序列)：
X(n) = ∑1<=K<=n( X(k)*X(n-k) ),即：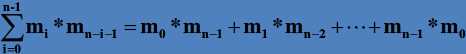
求和后得到：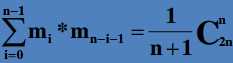
，结果也就是Catalan数(卡特兰数)(组合数学常用到的数列)。
栈混洗的甄别
首先若有一段序列：<1 2 3],其混洗后结果Catalan数计算可知有5种混洗情况，而其全排有6种，因此我们可以对其缺少的一种情况讨论。
这种情况就是[3 1 2>，为什么不可能出现呢，因为如果3要在混洗后放在栈B的底端，则需要在中介栈A中首先压入 1 2，然后压入3，这样，出栈的时候就只有 [3 2 1> 这种情况的序列，所以[3 1 2>是混洗后不可能出现的序列。(在这里，一般将这种经过栈混洗不存在的序列称为“禁形”)
“禁形”的图示为：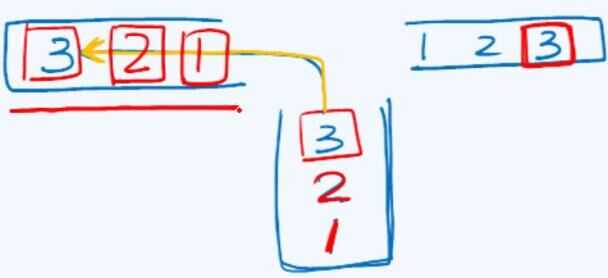
用数学方式表述后可以表述为：
需要注意的是，这种表述不仅是混洗后序列不存在的必要条件，而且还是充分条件。这一点已经在高德纳(Donald Ervin Knuth)的《计算机程序设计的艺术》(《The art of the computer programming》)中给出了正式解答。也就是说这一点可以作为栈混洗后的序列不存在的充要条件。
甄别算法
第一种算法：那么，有没有一个有效的算法甄别一个序列是否为另一个序列经过栈混洗得到呢，如果用上述结论，我们需要枚举每一个i，j，k元素，时间度为O(n3)。
第二种算法 : 其实这时我们这里仅仅有k=j+1也能完成这一判断，因为如果有一序列[4,1,2>,那么其中的3要么在4的左侧[3,4,1,2>，要么在右侧[4,3,1,2>,无论是哪种情况，我们仍然有[j+1,i,j>,因此这里我们可以只需枚举i,j两个元素，这样，时间度就为O(n2)。
第三种算法：那么还有更好的算法吗？答案是"有"，如果我们直接模拟这样一种栈混洗的过程，建立三个栈，先后完成push()...pop()...push()的操作，保证能依次得到目标序列，那么就可以确定这样的序列是可以得到的，反之就不能得到，这样的时间度最小为O(n)。
栈混洗与括号匹配
我们知道n对括号如果合法,诸如[ ( )( ( ) ( ) ) ][ ( )( ) ]这样的括号就是合法的，如何判别一个表达式中的n对括号是合法的呢，我们可以利用栈的思想，从左向右依次读取括号字符，如果这个括号是左括号，那么就将其压栈(push栈)，例如 ‘[‘ ，如果是与栈顶相匹配的右括号，例如 ‘]‘， 那么就将栈顶的元素出栈(pop掉)，如果不匹配或者最后栈不为空则这一段括号不合法。
那么这样的括号匹配过程和栈混洗又有怎样的关系呢，如下图所示：
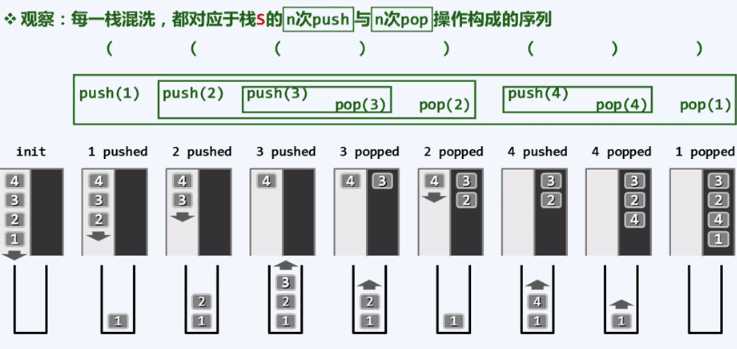
也就是说，对于n对括号，一次括号的合法判定过程就相当于一次合法栈混洗的过程，这两者一一対映，而且是一种双射关系，因此n对括号所组成的总表达式类型就相当于n个元素的栈混洗得到的序列数量。
即n个括号所组成的表达式类型总数就等于一个Catalan数。
原文：http://www.cnblogs.com/Inkblots/p/4947870.html