Lamertian模型是粗糙表面的理想反射模型,当光线照射到光滑表面会产生高光,Phong反射模型(Phong reflection model,1973)是其中一类的有向光照的镜面反射模型。
根据光的反射定律:入射光线与反射光线成相同角度。
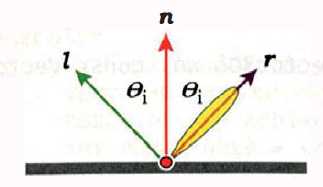
用\({l}\)表示入射光线,\({r}\)表示出射光线,\({n}\)表示物体表面法线,那么存在如下方程关系:
式①:\({r} = {al} + {bn}\)
上式中,\({a}\)和\({b}\)为常数项。对上式左右两边同乘\({n}\):
\({r \cdot n} = {al \cdot n} + {bn \cdot n}\)
得到式②:\({(1 - a)l \cdot n} = {b}\)
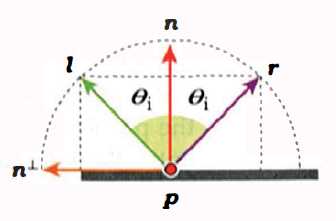
如果用\({n}^{\perp}\)表示与表面法线\({n}\)垂直的向量,那么\({l}\)与\({r}\)在\({n}^{\perp}\)上的投影应为相反的向量,\({r} = -{l}\):
\({r \cdot n^{\perp}} = {al \cdot n^{\perp}} + {bn \cdot n^{\perp}}\)
\({-l \cdot n^{\perp}} = {al \cdot n^{\perp}}\)
得:\({a} = -1\)
代入式①和式②中,可得\({r}\)的表达式:
\({r} = -{l} + {2(n \cdot l)n}\)
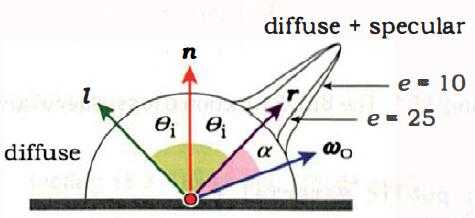
围绕在反射光线\({r}\)附近的反射辐射度应随\({\omega_o}\)与\({r}\)之间的夹角\({\alpha}\)的增加而减少。
Phong模型的镜面反射部分表示为\({\cos \alpha}^{e} = {r \cdot \omega_o}^{e}\),\(\alpha \in {[0, \frac{\pi}{2}]}\),\({\cos \alpha} \in {[0, 1]}\),\({e}\)与\(\alpha\)存在如下函数分布关系:
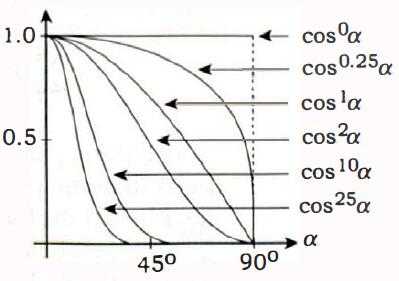
分布图中y轴代表\({e}\),x轴代表\(\alpha\),当\({e}\)增大时,随\(\alpha\)的增加而快速收敛。
至此可知Phong的BRDF高光项为:\({f_{r, s}(l, \omega_o)} = {k_s(r \cdot \omega_o)^{e}}\)
其中,\({k_s} \in [0, 1]\)表示为高光系数。
(未完待续)
原文:http://www.cnblogs.com/jerrycg/p/4948879.html