基于实例的学习方法中,最近邻法和局部加权回归法用于逼近实值或离散目标函数,基于案例的推理已经被应用到很多任务中,比如,在咨询台上存储和复用过去的经验;根据以前的法律案件进行推理;通过复用以前求解的问题的相关部分来解决复杂的调度问题。
基于实例方法的一个不足是,分类新实例的开销可能很大。这是因为几乎所有的计算都发生在分类时,而不是在第一次遇到训练样例时。所以,如何有效地索引训练样例,以减少查询时所需计算是一个重要的实践问题。此类方法的第二个不足是(尤其对于最近邻法),当从存储器中检索相似的训练样例时,它们一般考虑实例的所有属性。如果目标概念仅依赖于很多属性中的几个时,那么真正最“相似”的实例之间很可能相距甚远。
基于实例的学习方法中最基本的是k-近邻算法。这个算法假定所有的实例对应于n维欧氏空间Ân中的点。一个实例的最近邻是根据标准欧氏距离定义的。更精确地讲,把任意的实例x表示为下面的特征向量:
<a1(x),a2(x),an(x)>
其中ar(x)表示实例x的第r个属性值。那么两个实例xi和xj间的距离定义为d(xi, xj),其中:
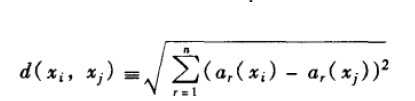


使用Python实现过程:
# -* -coding: UTF-8 -* -
import numpy
import operator
class kNN(object):
def __init__(self,filename):
self.filename = filename
def file_to_matrix(self):
"the last column is label"
fp = open(self.filename)
rows = len(fp.readlines())
result = numpy.zeros((rows,3))
labels = []
fp = open(self.filename)
index = 0
for line in fp.readlines():
fromline = line.strip()
linesplit = fromline.split(‘\t‘)
result[index,:] = linesplit[0:3]
labels.append(linesplit[-1])
index += 1
return result,labels
def data_standard(self,dataset):
‘‘‘data standardization
using (oldvalue - minvalue)/(maxvalue - minvalue)
the dataset is a matrix ,result is matrix too
‘‘‘
minvales = dataset.min(0)
maxvales = dataset.max(0)
ranges = maxvales - minvales
m = dataset.shape[0]
nordataset = dataset - numpy.tile(minvales, (m,1))
nordataset = nordataset/numpy.tile(ranges, (m,1))
return nordataset, minvales , ranges
def knn_classify(self,inputX,dataset,labels,k=3):
‘‘‘
calculation the distance,using ((a1 - b1)^2 + (a2 - b2)^2 + ... + (an - bn)^2)^0.5
result:
labels of the kth minimum distance
‘‘‘
rows = dataset.shape[0]
diffmat = numpy.tile(inputX, (rows , 1)) -dataset
square_dist = diffmat ** 2
"when axis=1 ,then rows sum;when axis=0 ,then cloumns sum;"
sum_square_dist = square_dist.sum(axis=1)
distance = sum_square_dist ** 0.5
"sorted distance , keep the position"
sorted_distance = distance.argsort()
labelcount = {}
for row in range(k):
votelabel = labels[sorted_distance[row]]
labelcount[votelabel] = labelcount.get(votelabel,0) + 1
sortedlabels = sorted(labelcount.iteritems() , key=operator.itemgetter(1), reverse=True)
return sortedlabels
if __name__ == ‘__main__‘:
testKNN = kNN(‘.\\datingTestSet.txt‘)
dataset, labels = testKNN.file_to_matrix()
nordataset, minvales , ranges=testKNN.data_standard(dataset)
fp = open(‘.\\datingTestSet.txt‘)
rows = len(fp.readlines())
errorcount = 0
fp = open(‘.\\datingTestSet.txt‘)
for i,line in enumerate(fp.readlines()):
fromline = line.strip().split(‘\t‘)
label = fromline[-1]
inputX = numpy.zeros((1,3))
inputX[:] = fromline[0:3]
sortedlabels = testKNN.knn_classify((inputX - minvales) / ranges,nordataset,labels,3)
if sortedlabels[0][0] == label :
#print ‘the ‘ + str(i) + ‘ is right \n‘
pass
else:
print ‘the %d record is error‘ %i
errorcount += 1
print ‘error count: %d‘ %errorcount
print ‘error ration: %f‘ %(float(errorcount) / rows)
距离加权最近邻算法
对k-近邻算法的一个显而易见的改进是对k个近邻的贡献加权,根据它们相对查询点xq的距离,将较大的权值赋给较近的近邻。例如,在表8-1逼近离散目标函数的算法中,我们可以根据每个近邻与xq的距离平方的倒数加权这个近邻的“选举权”。方法是通过用下式的公式来实现:
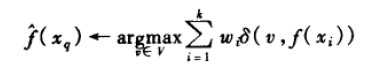
其中:
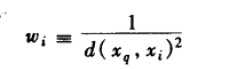
为了处理查询点xq恰好匹配某个训练样例xi,从而导致分母为0的情况,我们令这种情况下的 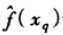 等于f(xi)。如果有多个这样的训练样例,我们使用它们中占多数的分类。
等于f(xi)。如果有多个这样的训练样例,我们使用它们中占多数的分类。
我们也可以用类似的方式对实值目标函数进行距离加权,只要用下式替换公式:
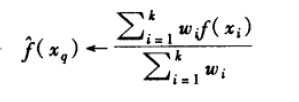
其中wi的定义与公式(8.3)中相同。注意公式(8.4)中的分母是一个常量,它将不同权值的贡献归一化(例如,它保证如果对所有的训练样例xi,f(xi)=c,那么 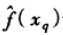 ----->c)。
----->c)。
注意以上k-近邻算法的所有变体都只考虑k个近邻以分类查询点。如果使用按距离加权,那么允许所有的训练样例影响xq的分类事实上没有坏处,因为非常远的实例对 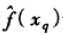 的影响很小。考虑所有样例的惟一不足是会使分类运行得更慢。如果分类一个新的查询实例时考虑所有的训练样例,我们称此为全局(global)法。如果仅考虑最靠近的训练样例,我们称此为局部(local)法。当公式(8.4)的法则被应用为全局法时,它被称为Shepard法(Shepard 1968)。
的影响很小。考虑所有样例的惟一不足是会使分类运行得更慢。如果分类一个新的查询实例时考虑所有的训练样例,我们称此为全局(global)法。如果仅考虑最靠近的训练样例,我们称此为局部(local)法。当公式(8.4)的法则被应用为全局法时,它被称为Shepard法(Shepard 1968)。
原文:http://www.cnblogs.com/tychyg/p/4954312.html