预处理:

判断一个串是不是回文串，往往要分开编写，造成代码的拖沓

int LongestPalindrome(const char * s, int n){
    int i, j, max;
    if (s == 0 || n < 1)
        return 0;
    max = 0;
    for (i = 0; i < n; ++i){//i is the middle point of palindrome
        for (j = 0; (i - j >= 0) && (i + j < n);++j)// for the lenth of palindrome is odd
        if (s[i - j] != s[i + j])
            break;
        if (--j * 2 + 1>max)    max = j * 2 + 1;
        for (j = 0; (i - j >= 0) && (i + j + 1 < n); ++j)//for the even case
        if (s[i - j] != s[i + j + 1])
            break;
        if (--j * 2 + 2 > max)
            max = j * 2 + 2;
    }
    return max;
}
void LongestPalindrome_test(){
    char s[] = "aba";
    int length = LongestPalindrome(s,strlen(s));
    cout << length << endl;
}

上面的循环中，对于回文长度本身的奇偶性，我们进行区别处理。这样有点拖沓。我们根据一个简单的事实：长度为n的字符串，共有n-1个“邻接”，加上首字符的前面后某字符的后面，共有n+1的“空（gap）”。因此，字符串本身和gap一起，共有2n+1个，必定是奇数。

• abba --> #a#b#b#a# 此回文这样处理后长度4-->9
• aba --> #a#b#c# 此回文这样处理后长度3-->7
  因此，将待计算母串扩展成gap串，则里面的回文字串的长度都变成了奇数，我们计算的时候只用考虑奇数匹配即可。

数组 int P[size]:

字符串12212321--> S[] = "$#1#2#2#1#2#3#2#1#";( 为了统一处理，最前面加一个特殊字符。则下标从1开始)
用一个数组P[i]来记录以字符S[i] 为中心的最长回文字串向左/向右扩张的长度(包括S[i]),比如S和P的对应关系:

S: "#    1    #    2    #    2    #    1    #    2    #    3    #    2    #    1    #";
P: {1    2    1    2    5    2    1    4    1    2    1    6    1    2    1    2     1}

P[i]-1正好是原字符串中回文串的总长度。

“# 1 # 2 # 2 # 1 #”
“---------1 2 3 4 5”
P[i] = 5
原始回文字符串长度是偶数的情况，则在gap串中P[i]的值多了中间的一个#。P[i]-1 == length

"# 1 # 2 # 3 # 2 # 1 # "
"---------------------1 2 3 4 5 6 "
p[i] = 6
原始回文字符串长度是奇数的情况，则在gap串种P[i]的值多了最后的#号。P[i]-1 == length
目前，只要知道了数组P的值，就能求得最多长回文的大小了。但是，怎么求呢P呢？请看下文。

如何求数组P：

S: "#    1    #    2    #    2    #    1    #    2    #    3    #    2    #    1    #";
P: {1    2    1    2    5    2    1    4    1    2    1    6    1    2    1    2     1}

我们的任务，假定已经得到了前i个值，考察i+1如何计算。即：在P[0...i-1]已知的情况下，利用其中信息，计算P[i]的值。

1. 通过简单遍历，找到i个三元组{k,P[k],k+p[k]},0<=k<=i-1。(以k为中心的字符形成的最大回文子串的最右位置是k+p[k]-1)
2. 以k+p[k]为关键字，挑选出这i个三元组中，k+p[k]最大的那个三元组，不妨记作（id,P[id],id+P[id]）。进一步，为了简化，记mx=P[id]+id，因此，得到三元组为（id，P[id],mx）,这个三元组的含义非常明显：所有i个三组中，向右达到最远的位置，就是mx。
3. 在计算P[i]的时候，考察i是否落在了区间[0,mx)中；
   -1. 若i在mx的右侧，说明[0,mx)没有能够控制住i，P[0..i-1]都已知，无法给P[i]的计算带来有价值的信息。
   -2. 若i在mx的左侧，说明[0,mx)控制（也有可能部分控制）了i，现在以图示来详细考察这种情况。这就是Manacher递推关系。

Manacher递推关系：

1. 记i关于id的对称点位j(j=2*id - i)，若此时满足条件mx-iP[j].
   记my为mx关于id的对称点();
   由于以S[id]为中心的最大回文字串为S[my+1...id...mx-1],
   即：S[my+1....,id]与S[id,...,mx-1]对称，而i和j关于id对称，因此P[i]=Pj。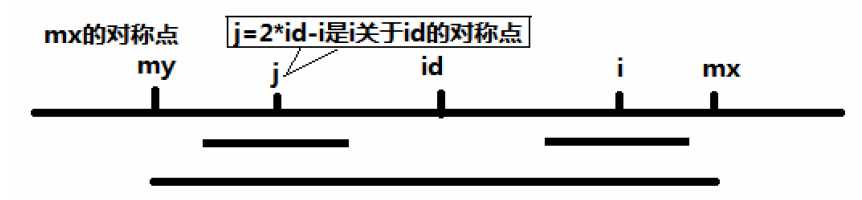
   

2. 记i关于id的对称点位j(),若此时满足条件mx-iP[j]:
   记my为mx关于id的对称点();
   由于以S[id]为中心得最大回文字串为S[my+1,...id...mx-1],即S[my+1,...,id]与S[id,...,mx-1]对称，而i和j关于id对称，因此P[i]至少等于mx-i（途中绿框部分）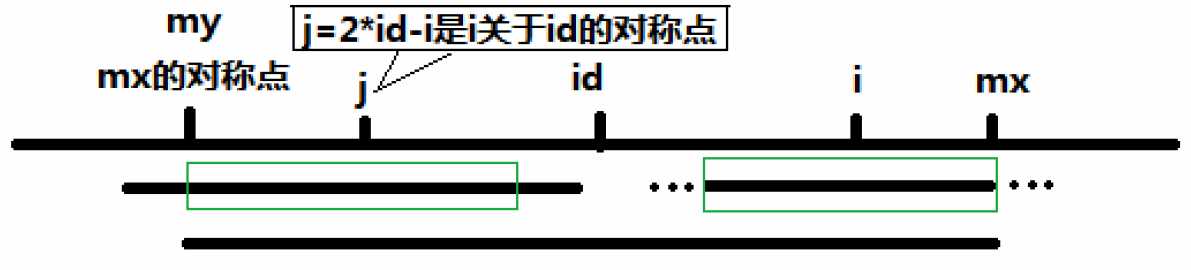
   

Manacher代码

void Manacher(char * s, int *p){
    int size = strlen(s);
    p[0] = 1;
    int id = 0;
    int mx = 1;
    for (int i = 1; i < size; i++){
        if (mx > i)    p[i] = min(p[2 * id - i], mx - i);
        else     p[i] = 1;
        /*
        这里计算s[i]处实际回文的长度，
        如果没有manacher算法，则这里p[i]每次都是从1开始
        而manancher算法利用了P[0...i-1]的信息，让i可能从大于1的地方开始*/
        for (; s[i - p[i]] == s[i + p[i]]; p[i]++);
        if (mx < i + p[i]){
            mx = i + p[i];
            id = i;
        }
    }
}
void Manacher_test(){
    char * s = "abbca2r";
    int size = (int)strlen(s);
    cout << s << endl;
    int sizenew = size * 2 + 2;//加上开始的$
    char * snew = new char[sizenew + 1];//别忘了最后的\0
    snew[0] = ‘$‘;
    int j = 0;
    for (int i = 1; i < 2 * size + 2; i++){
        if (i % 2 == 0)
            snew[i] = s[j++];
        else
            snew[i] = ‘#‘;
    }
    snew[sizenew] = ‘\0‘;
    cout << snew << endl;
    int * p = new int[sizenew];
    Manacher(snew,p);
    Print(p,sizenew);
}

Manacher的改进

p[j] > mx - i: p[i] = mx - i
p[j] < mx - i: p[i] = p[j]
p[j] = mx - i: p[i] >= p[j]
根据上面的源码，原始Manacher算法，前两个等号都是大于等于。
下面是改进的Manacher算法：

void Manacher2(char * s, int * p){
    int size = strlen(s);
    p[0] = 1;
    int id = 0;
    int mx = 1;
    for (int i = 1; i < size; i++){
        if (mx>i){
            if (mx > i){
                if (p[2 * id - 1] != mx - i){
                    p[i] = min(p[2*id - i],mx-i);    //能确定p[i]的值
                }
                else{
                    p[i] = p[2*id - i];
                    for (; s[i - p[i]] == s[i + p[i]]; p[i]++);
                }
            }
        }
        else{
            p[i] = 1;
            for (; s[i - p[i]] == s[i + p[i]]; p[i]++);
        }
        if (mx < i + p[i]){
            mx = i + p[i];
            id = i;
        }
    }
}

最长回文Manacher

原文：http://www.cnblogs.com/gavin-yue/p/4975665.html