| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 2378 | Accepted: 1041 |
Description
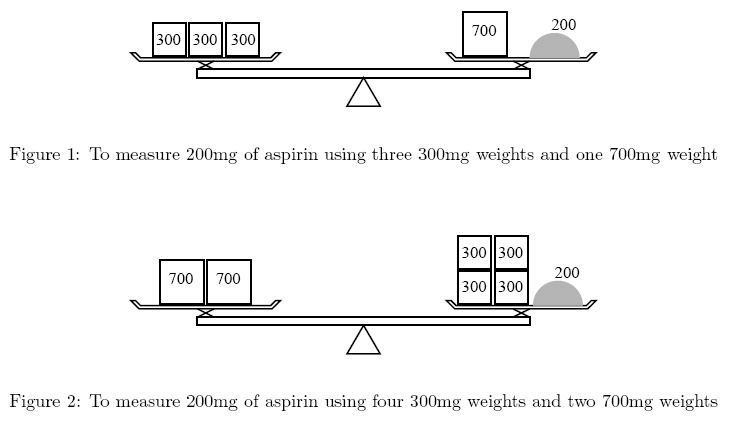
Input
Output
Sample Input
700 300 200 500 200 300 500 200 500 275 110 330 275 110 385 648 375 4002 3 1 10000 0 0 0
Sample Output
1 3 1 1 1 0 0 3 1 1 49 74 3333 1
题目描述
一个人有一种天平,这种天平只有两种重量的砝码 a 和 b,现在要称出重量为 c 的物品,问你至少需要多少 a 和
b,答案需要满足 a 的数量加上 b 的数量和最小,
并且他们的重量和也要最小。(两个盘都可以放砝码)
分析
假设 a 砝码我们用了 x 个,b 砝码我们用了 y 个。那么天平平衡时,就应该满足ax+by==c。x,y 为正时表示放在和 c
物品的另一边,为负时表示放在 c 物品的同一边。
于是题意就变成了求|x|+|y|的最小值了。x 和 y 是不定式 ax+by==c
的解。刚刚上面已经提到了关于 x,y 的所以解的同式,即
x=x0+b/d*t
y=y0-a/d*t
穷举所有解,取|x|+|y|最小的?显然是行不通的,仔细分析:
|x|+|y|==|x0+b/d*t|+|y0-a/d*t|,我们规定
a>b(如果 a<b,我们便交换 a
b),从这个式子中,
我们可以轻易的发现:|x0+b/d*t|是单调递增的,|y0-a/d*t|是单调递减的,而由于我们规定了
a>b,
那么减的斜率边要大于增的斜率,于是整个函数减少的要比增加的快,但是由于绝对值的符号的作用,最终函数还是递增的。
也就是说,函数是凹的,先减小,再增大。那么什么时候最小呢?很显然是
y0-a/d*t==0 的时候,
于是我们的最小值|x|+|y|也一定是在 t=y0*d/a附近了,只要在附近枚举几个值就能找到最优解了。

1 /* 2 POJ-2142The Balance 3 拓展欧几里德算法 4 */ 5 #include <iostream> 6 #include <stdio.h> 7 #include <cstring> 8 #include <cmath> 9 #include <algorithm> 10 //#define int 0x7fffffff 11 using namespace std; 12 13 int exgcd(int a,int b,int &x,int &y) 14 { 15 if(b==0) 16 { 17 x=1; 18 y=0; 19 return a; 20 } 21 int d=exgcd(b,a%b,x,y); 22 int t=x; 23 x=y; 24 y=t-(a/b)*y; 25 return d; 26 } 27 int main() 28 { 29 int a,b,c,x,y,d,x1,y1,ansx,ansy,i; 30 bool sf; 31 while(scanf("%d %d %d",&a,&b,&c)!=EOF) 32 { 33 if(a==0||b==0||c==0) 34 break; 35 sf=false; 36 if(a<b) 37 { 38 sf=true; 39 swap(a,b); 40 } 41 d=exgcd(a,b,x,y); 42 x*=(c/d); 43 y*=(c/d); 44 int t=y*d/a; 45 ansx=abs(x+t*b/d); 46 ansy=abs(y-t*a/b); 47 for(i=1;i<5;i++) 48 { 49 x1=x+(t+i)*b/d; 50 y1=y-(t+i)*a/d; 51 x1=abs(x1); 52 y1=abs(y1); 53 if(x1+y1<ansx+ansy||(x1+y1==ansx+ansy&&x1*a+y1*b<ansx*a+ansy*b)) 54 { 55 ansx=x1; 56 ansy=y1; 57 } 58 x1=x+(t-i)*b/d; 59 y1=y-(t-i)*a/d; 60 x1=abs(x1); 61 y1=abs(y1); 62 if(x1+y1<ansx+ansy||(x1+y1==ansx+ansy&&x1*a+y1*b<ansx*a+ansy*b)) 63 { 64 ansx=x1; 65 ansy=y1; 66 } 67 } 68 if(sf) 69 swap(ansx,ansy); 70 printf("%d %d\n",ansx,ansy); 71 } 72 return 0; 73 }
POJ-2142The Balance,布布扣,bubuko.com
原文:http://www.cnblogs.com/vivider/p/3652719.html