hdu1452 Happy 2004

原题：http://acm.hdu.edu.cn/showproblem.php?pid=1452

等比数列求和公式：（之前忘记了。+ =）

奇性函数：

在数论中，积性函数是指一个定义域为正整数n 的算术函数f(n)，有如下性质：f(1) = 1，且当a 和b 互质时，f(ab) = f(a) f(b)。

若一个函数f(n) 有如下性质：f(1) = 1，且对两个随意正整数a 和b 而言，不只限这两数互质时，f(ab) = f(a)f(b) 都成立，则称此函数为完全积性函数。

在数论以外的其他数学领域中所谈到的积性函数通常是指完全积性函数。

例子

• φ(n) －欧拉φ函数，计算与n互质的正整数之数目
• μ(n) －默比乌斯函数，关于非平方数的质因子数目
• gcd(n,k) －最大公因子，当k固定的情况
• (n): 除数函数，n的所有正因子的k次幂之和，当中k可为任何复数。在特例中有：
  • (n) = d(n) - n的正因子数目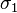
  • (n) = (n) - n的所有正因子之和
• 1(n) －不变的函数，定义为 1(n)=1 （完全积性）
• Id(n) －单位函数，定义为 Id(n)=n （完全积性）
• Id_k(n) －幂函数，对于任何复数、实数k，定义为Id_k(n) = n^k （完全积性）
  • Id₀(n) = 1(n) 及
  • Id₁(n) = Id(n)
• ε(n) －定义为：若n = 1，ε(n)=1；若n > 1，ε(n)=0。有时称为“对于狄利克雷卷积的乘法单位”（完全积性）
• (n/p) －勒让德符号，p是固定质数（完全积性）
• λ(n) －刘维尔函数，关于能整除n的质因子的数目
• γ(n)，定义为γ(n)=(-1)^ω(n)，在此加性函数ω(n)是不同能整除n的质数的数目
• 所有狄利克雷特征均是完全积性的
• 
  

可见本题目为：除数函数，不完全奇性函数。

const int INF=0x3f3f3f3f;  另外参见了大神的代码，发现最大值可以这么表示。

//============================================================================
// Name        : Math_hdu1452.cpp
// Author      : vit
// Version     :
// Copyright   : Your copyright notice
// Description : Hello World in C++, Ansi-style
//============================================================================

#include <iostream>
#include <stdio.h>
#include <string.h>

#define MOD 29

using namespace std;

int pow(int a,int b)
{
    int ans=1;
    while(b)
    {
        if(b&1)//judge odd or even
        	ans = (ans * a) % MOD;
        a = a * a % MOD;
        b=b>>1;
    }
    return ans;
}


int main() {
	int x;
	int a, b, c;
	while(cin >> x && x){
		a = (pow(2,2*x + 1) - 1) * 1 % MOD;
		b = (pow(3,x + 1) - 1) * 15 % MOD;
		c = (pow(167, x + 1) - 1) * 18 % MOD;

		cout << a * b * c % MOD << endl;
	}
	return 0;
}

hdu1452 Happy 2004,布布扣,bubuko.com

hdu1452 Happy 2004

原文：http://blog.csdn.net/svitter/article/details/23205327