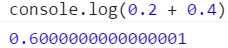
在上一章『浮点数(从惊讶到思考)』中我们讲到用浮点数表示 数 时出现的问题——很多数都 不能表示。(注意浮点数表示的是数,而不仅仅是小数。)
在浮点数的表示范围内,有多于 99.999...% 的数在计算机中是 不能表示 的。
请注意我使用的措辞,区别开 不能表示 和 不能精确表示。
下面我从数量级分析一下,32bit 浮点数的表示范围是 10 的 38 次方,而表示个数呢,是 10 的 10 次方。 能够被表示的数只有 1/100000000.... (大概有30个零),这个数多大呢?还记得那个国际象棋和麦子的故事吗?
有一张很大很大的纸,对折 38 次,会有多高呢? 一米?一百米?比珠峰还高?它不仅仅比珠峰高,其实它已经快到达月球了。
回到原来的话题,还有更残忍的真相。 在剩下的可以表示的不到 0.000...1% 的数中,又有多少不能精确表示呢?
上一章中我还给出了一种用定点数精确表示小数的方法。 事实上,手持计算器、java 中的 BigDecimal、C# 中的货币类型、MySQL 中的 NUMERIC 类型就是这么干的。 你还记得在数据库中添加字段时的 SQL 语句是如何写的吗?
这篇博客我将为大家讲解为什么很多数 不能精确表示。
要把小数装入计算机,总共分几步?
在上面的第一步和第三步都有可能 丢失精度。
下面我们讨论如何把十进制小数转换成二进制小数。
考虑我们将 1/7(七分之一) 写成小数的时候是如何做的?
用 1 除以 7,得到的商就是小数部分,剩下的余数我们继续除以 7,一直除到什么时候结束呢? 有两种情况:
如果余数为 0, 结束了.
当除到某一步时,余数等于 1… 余数如果为 1 的话,再继续除下去,不就又是 1/7 了吗?它永远不会结束,它循环了。
圆周率,无限——却永不重复。
那么 0.1 在计算机中可以精确表示吗?
答案是出人意料的, 不能。
在此之前,先思考个问题: 在 0.1 到 0.9 的 9 个小数中,有多少可以用二进制精确表示呢?
我们按照乘以 2 取整数位的方法,把 0.1 表示为二进制(我假设那些不会进制转换的同学已经补习完了):
(1) 0.1 x 2 = 0.2 取整数位 0 得 0.0
(2) 0.2 x 2 = 0.4 取整数位 0 得 0.00
(3) 0.4 x 2 = 0.8 取整数位 0 得 0.000
(4) 0.8 x 2 = 1.6 取整数位 1 得 0.0001
(5) 0.6 x 2 = 0.2 取整数位 1 得 0.00011
(6) 0.2 x 2 = 0.4 取整数位 0 得 0.000110
(7) 0.4 x 2 = 0.8 取整数位 0 得 0.0001100
(8) 0.8 x 2 = 1.6 取整数位 1 得 0.00011001
(9) 0.6 x 2 = 1.2 取整数位 1 得 0.000110011
(n) ...
我们得到一个无限循环的二进制小数 0.000110011... 这就是0.1 无法在计算机中用二进制精确表示的原因
0.1 到 0.9 的 9 个小数中,只有 0.5 可以用二进制精确的表示。
如果把 0.0 再算上,那么就有两个数可以精确表示,一个奇数 0.5,一个偶数 0.0。 为什么是两个呢?因为计算机二呗,其实计算机还真够二的。
世界上有 10 种人,一种是懂二进制的,一种是不懂二进制的。
其实答案很显然,我再领大家换个角度思考,0.5 就是一半的意思。 在十进制中,进制的基数是 10,而 5 正好是 10 的一半。 2 的一半是多少?当然是 1 了。 所以,十进制的 0.5 就是二进制的 0.1。如果我用八进制呢? 不用计算你就应该立刻回答:0.4;转换成十六进制呢,当然就是 0.8 了。
(0.5)10 = (0.1)2 = (0.4)8 = (0.8)16
如果你还想继续思考,就又会发现一个有趣的事实,我们称之为 定理A。 我们上面的数,都是小数点后面一位小数,因此,在十进制中,这样的小数有 10 个(就是 0 到 9); 同理,在二进制中,如果我们让小数点后面有一位小数,应该有多少个呢?当然是 2 个了(0 和 1)。
哇,好像发现了新大陆一样,很兴奋是吧。那我再给你一棒,其实定理A是错的。再重申一遍 尽信书,则不如无书。我写博客的目的 不是把我的思想灌输到你的脑子里,你应该有自己的思想,自己的思考方式,当我得出这个结论时,你应该立刻反驳我:“按照你的思路,如果是 16 进制的话,应该可以精确表示所有的 0.1 到 0.9 的数甚至还可以精确表示其它的 6 个数。而事实呢,16 进制可以精确表示的数 和 2 进制可以精确表示的数是一样的,只能精确表示 0.5。”
那么到底怎么确定一个数能否精确表示呢?还是回到我们熟悉的十进制分数。
1/2、5/9、34/25 哪些可以写成有限小数?把一个分数化到最简(分子分母无公约数),如果分母的因式分解只有 2 和 5,那么就可以写成有限小数,否则就是无限循环小数。为什么是 2 和 5 呢?因为他们是 10 的因子 10 = 2 x 5。
二进制和十六进制呢?他们的因子只有 2,所以十六进制只是二进制的一种简写形式,它的精度和二进制一样。
如果一个十进制数可以用二进制精确表示,那么它的最后一位肯定是 5。
备注:这是个必要条件,而不是充分条件。一位热心网友设计出了下面的解决精度的方案。我就不解释了,同学们自己思考一下吧。
我有一个观点,针对小数精度不够的问题(例如 0.1),软件可以人为的在数据最后一位补 5, 也就是 0.15,这样牺牲一位,但是可以保证数据精度,还原再把那个尾巴 5 去掉。
请同学们思考一下。
一位热心网友 独孤小败 在 OSC 上回复了我上一篇文章,提出了一个疑问:
在 java 中计算 0.2 + 0.4 得到的结果是
// 代码(a)
double d = 0.2 + 0.4; // 结果是 0.6000000000000001
但是当直接输出 0.6 的时候,确实是 0.6
// 代码(b)
double d = 0.6; // 结果是 0.6
好像很矛盾。很显然,通过代码(b)可以知道,在 java 中,可以精确 显示 0.6,哪怕 0.6 不能被精确表示,但至少能精确把 0.6 显示出来,这不是和代码(a)矛盾了吗?
这又是一个 想当然的错误,在直观上认为 0.2 + 0.4 = 0.6 是必然成立的(在数学上确实如此),既然(a)的结果是 0.6,而且 java 可以精确输出 0.6,那么代码(a)的结果应该输出 0.6。
其实在计算机上 0.2 + 0.4 根本就不等于 0.6 (为什么?可以查看本系列『运算符』),因为 0.2 和 0.4 都不能被精确表示。 浮点数的精度丢失在每一个表达式,而不仅仅是表达式的求值结果。
我们用数学中的概念类比一下,比如四舍五入,我们计算 1.6 + 2.8 保留整数。
1.6 + 2.8 = 4.4
四舍五入得到 4。我们用另一种方法
先把 1.6 四舍五入为 2
再把 2.8 四舍五入为 3
最后求和 2 + 3 = 5
通过两种运算,我们得到了两个结果 4 和 5。同理,在我们的浮点数运算中,参与运算的两个数 0.2 和 0.4 精度已经丢失了,所以他们求和的结果已经不是 0.6 了。
上面一直在讨论小数,整数呢?在博客园,一位童鞋为下面的代码抓狂了:
JSON.parse(‘{"status":1,"id":9986705337161735,"name":"test"}‘).id;
把这段代码复制到 Chrome 的 Console 中,按回车, 诡异的问题出现了 9986705337161735 居然变成了 9986705337161736!原始数据加了 1。
9986705337161735
9986705337161736
一开始以为是溢出,换了个更大的数:9986705337161738 发现不会出现这个问题。
但是 9986705337161739 输出又变成了 9986705337161740!
9986705337161739
9986705337161740
测试几次之后发现浏览器输出数字的一个规律(justjavac注:其实这个规律是错误的):
又多测了几次,发现根本没有规律,很混乱!!有时候是加,有时候是减!!
原文:http://www.cnblogs.com/abapscript/p/4995143.html