1、这道题学了个单词,product 还有 乘积 的意思。。
题意就是在一个 m*n的矩阵中,放入L个敌军的伞兵,而我军要在伞兵落地的瞬间将其消灭。现在我军用一种激光枪组建一个防御系统,这种枪可以安装在一行(或者一列),并且安装在不同行(或者不同列)的费用是不一样的,枪的攻击范围是一行(或者一列)。安装所有枪的费用是它们每个费用的“乘积”,现在求组建这个系统需要的最小费用。
2、与前面做的二分图的一道题有点相似(POJ - 3041 Asteroids(最小点覆盖数))。但是现在这道题在不同行(或者不同列)的费用不同,所以还是有区别的。(ps:也就是说,之前那个把费用都设为1,也可以用这道题的方法来做?应该是的。)
建图:与上述的题类似,把行、列分别拆出来,分别作为二分图的X集、Y集中的点即可。然后在所建的二分图上加入超级源点(_S)、超级汇点(_T),再求最大流。
为什么求的最大流保证费用最小呢?因为对应二分图(加入源点、汇点后)中,总是选的_S->u 和v->_T 中的费用小的(即流量小的),并且覆盖了中间所有边(即不加源点、汇点前的二分图中的所有边)(好像是~,未证明)。
这里因为求的是乘积,所以用对数转化下:建图时,流量为 log(cost)即对各个cost求自然对数;再求出最大流maxflow,最后求 e^maxflow。(因为a*b*c=e^(loga+logb+logc);)
下面对题目样例作个解释:可忽略。
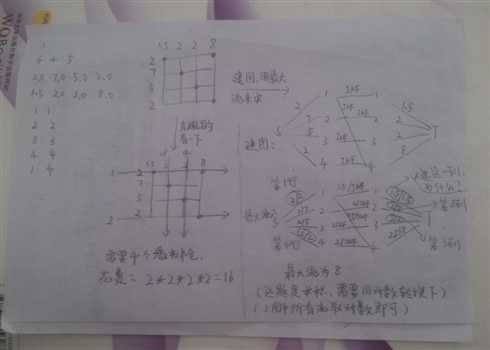
图中最大流的那个图里,画圈圈的是这条边满流(自己起的名,例:2/2),也就是有可能选的某行或某列(我是这么理解的),也就是说有可能不选它(例:1.5/1.5)。
下面解释样例为什么不选1.5/1.5而选2/2(即不选第1列而选第1行),因为选第1列的话,必须同时选第4列,才能代替选第1行和第4行,经比较,费用变大,所以不选。
对这种怎么选的情况,举个栗子,如图:
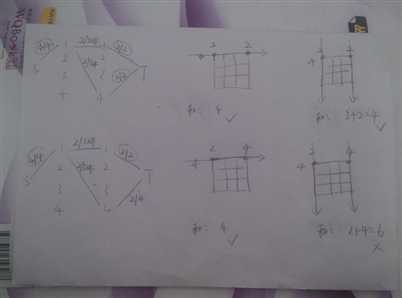
上面的为可替代的情况,
下面的为不可替代的情况。
3、
3、ISAP邻接表形式:直接用的这个速度比较好的模板

#include<iostream> #include<stdio.h> #include<string.h> #include<math.h> using namespace std; const int MAXN=128;//点数的最大值 const int MAXM=1500;//边数的最大值(加的双向加,所以是2倍,别忘了加上超级源点和超级汇点) const int INF=0x3f3f3f3f; struct Edge{ int to,next; double cap,flow; }edge[MAXM];//注意是MAXM int tol; int head[MAXN]; int gap[MAXN],dep[MAXN],pre[MAXN],cur[MAXN]; void init(){ tol=0; memset(head,-1,sizeof(head)); } //加边,单向图三个参数,双向图四个参数 void addedge(int u,int v,double w,double rw=0){ edge[tol].to=v;edge[tol].cap=w;edge[tol].next=head[u]; edge[tol].flow=0;head[u]=tol++; edge[tol].to=u;edge[tol].cap=rw;edge[tol].next=head[v]; edge[tol].flow=0;head[v]=tol++; } //输入参数:起点、终点、点的总数 //点的编号没有影响,只要输入点的总数 double sap(int start,int end,int N){ memset(gap,0,sizeof(gap)); memset(dep,0,sizeof(dep)); memcpy(cur,head,sizeof(head)); int u=start; pre[u]=-1; gap[0]=N; double ans=0; while(dep[start]<N){ if(u==end){ double Min=INF; for(int i=pre[u];i!=-1;i=pre[edge[i^1].to]) if(Min>edge[i].cap-edge[i].flow) Min=edge[i].cap-edge[i].flow; for(int i=pre[u];i!=-1;i=pre[edge[i^1].to]){ edge[i].flow+=Min; edge[i^1].flow-=Min; } u=start; ans+=Min; continue; } bool flag=false; int v; for(int i=cur[u];i!=-1;i=edge[i].next){ v=edge[i].to; if(edge[i].cap-edge[i].flow&&dep[v]+1==dep[u]){ flag=true; cur[u]=pre[v]=i; break; } } if(flag){ u=v; continue; } int Min=N; for(int i=head[u];i!=-1;i=edge[i].next) if(edge[i].cap-edge[i].flow&&dep[edge[i].to]<Min){ Min=dep[edge[i].to]; cur[u]=i; } gap[dep[u]]--; if(!gap[dep[u]])return ans; dep[u]=Min+1; gap[dep[u]]++; if(u!=start)u=edge[pre[u]^1].to; } return ans; } int main(){ int T; int m,n,L; double ri,ci; int _S,_T;//超级源点,超级汇点 int r,c; scanf("%d",&T); while(T--){ init(); scanf("%d%d%d",&m,&n,&L); _S=m+n; for(int i=0;i<m;++i){ scanf("%lf",&ri); addedge(_S,i,log(ri)); } _T=m+n+1; for(int i=0;i<n;++i){ scanf("%lf",&ci); addedge(m+i,_T,log(ci)); } for(int i=0;i<L;++i){ scanf("%d%d",&r,&c); addedge(r-1,m+c-1,INF); } printf("%.4f\n",exp(sap(_S,_T,m+n+2))); } return 0; }
原文:http://www.cnblogs.com/bofengyu/p/5002592.html