在学习了机器学习十大算法之后,我决定将目光投向神经网络,从而攀登深度学习的高峰。这条险路的第一个拦路虎就是Rosenblatt感知器。为什么这么说呢?不仅是因为它开拓性的贡献——感知器是第一个从算法上完整描述的神经网络,而Rosenblatt感知器是感知器作为监督学习的第一个模型。还因为学习Rosenblatt感知器能够帮助了解神经元的结构、信息流的传递以及知识的学习和存储,从而打开看待问题的全新视角——模拟人脑解决问题。当然,仅仅如此的话,它只能说是可口的羔羊,谈不上拦路的猛虎。自然是在理解这一问题时遇到了难处:1)Rosenblatt感知器为什么能收敛?《神经网络与机器学习》中的证明并不理想,它忽略了学习率和初始权重向量的影响;2)学习率和初始权重向量对迭代次数的影响是什么?3)它的更新过程与梯度下降法如此相似,不禁想问两者之间有何联系?4)线性可分两类问题通常在寻找一个分割超平面,Rosenblatt感知器也不例外,能否将这个超平面可视化,从而帮助理解?看!这真的是一个威风凛凛的猛虎,但它吓不倒人。下面开始我们的打虎过程。
认识这只虎——Rosenblatt感知器的结构
介绍感知器就不得不谈神经元的结构。神经元由突触、响应器、激活函数组成,顺序响应输入信号,最终获得输出结果。如图1所示,首先,输入信号的每一个分量由突触加权,再与偏置一起由响应器求和,之后通过激活函数获得输出。
响应器对突触加权后的信号和偏置求和,得到响应值:
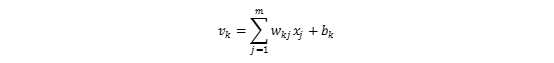
常用的激活函数有阈值函数,Sigmoid函数和tanh函数。为纪念McCulloch和Pitts(1943)的开拓性工作,激活函数为阈值函数的神经元也被称为McCulloch-Pitts模型,此时:
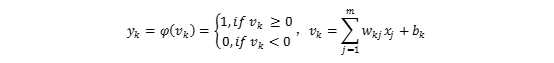
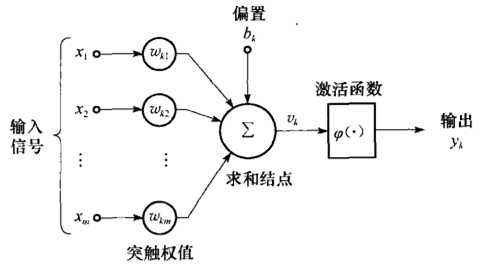
图1 神经元结构
Rosenblatt感知器建立在McCulloch-Pitts神经元模型上,以解决线性可分的两类问题。两类记为{+1,-1},此时:
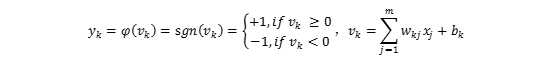
在神经元进行学习分类问题时,每一个样本都将作为一个刺激传入神经元。输入信号是每一个样本的特征,期望的输出是该样本的类别。当输出与类别不同时,我们将调整突触权值,直到每个样本的输出与类别相同。
老虎要发威——Rosenblatt感知器的更新过程
到目前为止,我们了解了Rosenblatt感知器的工作流程,但还没有解释它如何对于误分类的刺激调整权重值。在此之前,我们先定义输入的数据,方便后续的描述及推导。假设我们的样本采自m维空间Rm,每个样本由特征值和类别组成,记为X,于是:
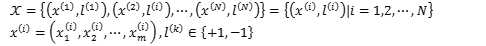
当我们挑选样本x(k)(第k个刺激并不等于第k个样本,同一个样本可能反复成为刺激)刺激神经元时,有:
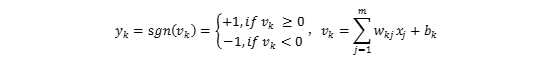
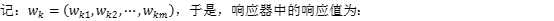
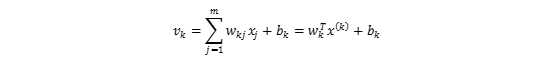
为了让上式更为简洁,我们将x(k)和wk增加一维:
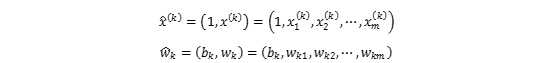
此时:
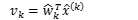
神经元对刺激x^(k)的输出为:
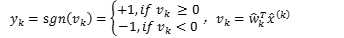

到这里,我们完成了对Rosenblattt感知器的推导,其伪代码为:

老虎会防御——谜一样的感知器收敛原理
Rosenblatt感知器对于线性可分的两类问题总是有效的,但采用的方式与高斯分类器、逻辑回归、决策树还有SVM截然不同。那么能否保证它对所有线性可分的两类问题都能收敛?下面将利用夹逼定理对收敛性进行证明。
下界

上界

不等式左边是一个开口向上的一元二次方程,因此必存在,使等式不成立,因此该方法收敛。
老虎怂了——初始权重向量和学习率的影响


老虎搬救兵——感知器背后的随机梯度下降法
如果学习过随机梯度下降法的话,我们就会发现Rosenblatt感知器与随机梯度下降法间的相似度。
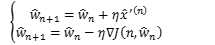
如果我们对Rosenblatt感知器构造损失函数
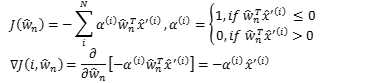
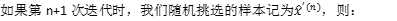
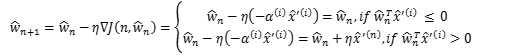
因此,Rosenblatt感知器的迭代过程实际上是随机梯度下降法的一个简化。由于随机梯度下降法依期望收敛,Rosenblatt感知器也是收敛的。
老虎被参观——Rosenblatt感知器的可视化过程

因此,Rosenblatt感知器可理解为:1)将特征增加一维,新的一维为1,对应神经元中的偏置;2)增维后的特征与样本类别相乘,得到校正后的特征向量;3)寻找一个权重向量,其与所有校正后的特征向量的夹角小于90度。以一维空间的样本为例,
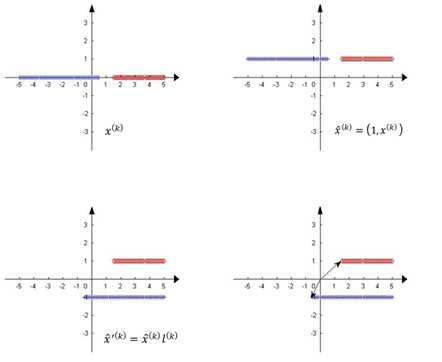
图2 对特征空间进行升维和标签校正
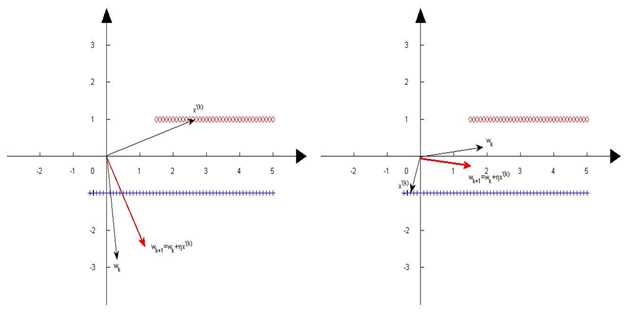
图3 权重向量的更新过程
当权重向量与特征向量夹角大于90度时,调整权重向量,减少两者夹角。最终使其对所有的特征向量夹角都小于90度,实现对样本的正确分类。
打虎心得——最后的总结
最开始学Rosenblatt感知器时,只是想把收敛原理搞清楚,但搞懂之后,有两点是之前没有预料到的:1)它隐含一个损失函数,而这个损失函数不需要像逻辑回归一样由一个logit函数进行转换;2)之前对线性可分停留在可以找到一个超平面,左边一类,右边一类。但对于超平面与样本之间有何联连并不清楚,现在明白两者对应m+1维空间两个夹角小于90度的超平面。
好了,打虎到此结束,有缘再会。
原文:http://www.cnblogs.com/lanix/p/5003521.html