三向切分快速排序算法是对快速排序算法的一个改进。快速排序算法是一种二切分的算法,但存在潜在的缺点:在切分不平衡时这个算法可能会极为低效。
快速三向切分的原理
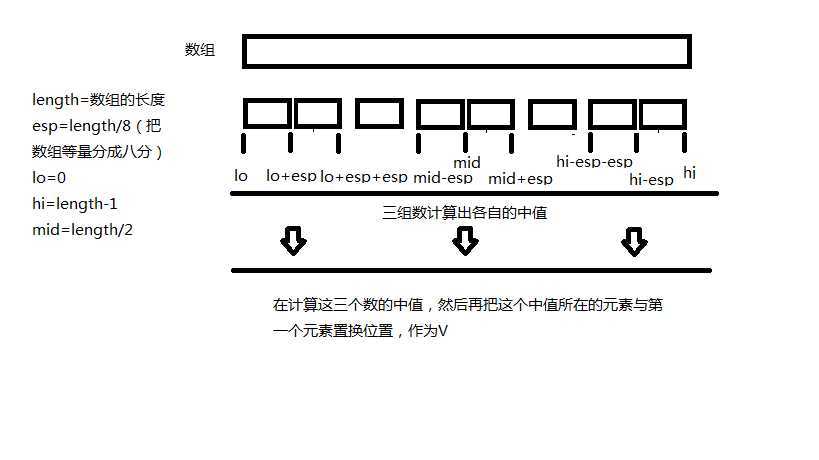
把通过上面的方法计算出中值并在作为一个参照或支点
排序过程中 i 从数组开头遍历把与中值相等的元素放在 lo 和 p 中间,小于中值的元素放在 p 和 i 中间,j 从数组开头遍历把与中值相等的元素放在 hi 和 q 中间,大于中值的元素放在 hi 和 j 中间
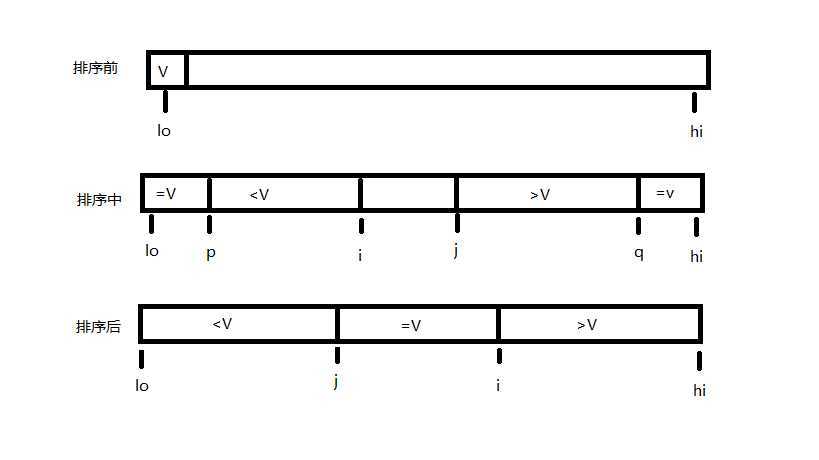
排序后,再把 lo 和 j ,hi 和 i 间的元素按照上述方法递归排序。
下面是JAVA实现
当数组元素不多的情况下快速排序的算法比插入排序的算法效率低,因此设置CUTOFF这个值,当数组长度小于CUTOFF,就使用插入排序。当数组长度小于40的时候使用后快速排序,当数组长度大于40的时候使用快速三向切分排序。
其中的快速排序算法也采用计算中值的方式。
public class QuickX { private static final int CUTOFF = 8; // cutoff to insertion sort, must be >= 1 // This class should not be instantiated. private QuickX() { } /** * Rearranges the array in ascending order, using the natural order. * @param a the array to be sorted */ public static void sort(Comparable[] a) { sort(a, 0, a.length - 1); } private static void sort(Comparable[] a, int lo, int hi) { int N = hi - lo + 1; // cutoff to insertion sort if (N <= CUTOFF) { insertionSort(a, lo, hi); return; }else if (N <= 40) { // use median-of-3 as partitioning element int m = median3(a, lo, lo + N/2, hi); // check the value of the median System.out.println("the value of the median: "+a[m]); exch(a, m, lo); }else { // use Tukey ninther as partitioning element int eps = N/8; int mid = lo + N/2; int m1 = median3(a, lo, lo + eps, lo + eps + eps); int m2 = median3(a, mid - eps, mid, mid + eps); int m3 = median3(a, hi - eps - eps, hi - eps, hi); int ninther = median3(a, m1, m2, m3); // check the value of the ninther median System.out.println("the value of the ninther median: "+a[ninther]); exch(a, ninther, lo); } // Bentley-McIlroy 3-way partitioning int i = lo, j = hi+1; int p = lo, q = hi+1; Comparable v = a[lo]; while (true) { while (less(a[++i], v)) if (i == hi) break; while (less(v, a[--j])) if (j == lo) break; // pointers cross if (i == j && eq(a[i], v)) exch(a, ++p, i); if (i >= j) break; exch(a, i, j); if (eq(a[i], v)) exch(a, ++p, i); if (eq(a[j], v)) exch(a, --q, j); } //check the situation during a sort System.out.print("during:>"); show(a); System.out.println(); i = j + 1; for (int k = lo; k <= p; k++) exch(a, k, j--); for (int k = hi; k >= q; k--) exch(a, k, i++); //check the situation during a sort System.out.print("after:>"); show(a); System.out.println(); sort(a, lo, j); sort(a, i, hi); } // sort from a[lo] to a[hi] using insertion sort private static void insertionSort(Comparable[] a, int lo, int hi) { for (int i = lo; i <= hi; i++) for (int j = i; j > lo && less(a[j], a[j-1]); j--) exch(a, j, j-1); } // return the index of the median element among a[i], a[j], and a[k] private static int median3(Comparable[] a, int i, int j, int k) { return (less(a[i], a[j]) ? (less(a[j], a[k]) ? j : less(a[i], a[k]) ? k : i) : (less(a[k], a[j]) ? j : less(a[k], a[i]) ? k : i)); } /*************************************************************************** * Helper sorting functions. ***************************************************************************/ // is v < w ? private static boolean less(Comparable v, Comparable w) { return v.compareTo(w) < 0; } // does v == w ? private static boolean eq(Comparable v, Comparable w) { return v.compareTo(w) == 0; } // exchange a[i] and a[j] private static void exch(Object[] a, int i, int j) { Object swap = a[i]; a[i] = a[j]; a[j] = swap; } /*************************************************************************** * Check if array is sorted - useful for debugging. ***************************************************************************/ private static boolean isSorted(Comparable[] a) { for (int i = 1; i < a.length; i++) if (less(a[i], a[i-1])) return false; return true; } // print array to standard output private static void show(Comparable[] a) { for (int i = 0; i < a.length; i++) { System.out.print(a[i]+" "); } } /** * Reads in a sequence of strings from standard input; quicksorts them * (using an optimized version of quicksort); * and prints them to standard output in ascending order. */ public static void main(String[] args) { String[] a = {"a","d","e","d","r","x","r","e","f","x","u", "o","p","z","c","b","h","l","t","v","a","q","g", "c","u","r","y","m","b","n","w","w","v","x","z", "o","b","a","d","e","d","r","x","r","e","f","x", "o","p","z","c","b","h","l","t","v","a","q","g", "c","u","r","y","m","b","n","w","w","v","x","z", }; QuickX.sort(a); System.out.print("finish:>"); show(a); } }
输出情况:
the value of the ninther median: o
during:>o o e d n b m e f c g a l h c b h l b c a d g c f e d m b n e d a b a z x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x o
after:>a b e d n b m e f c g a l h c b h l b c a d g c f e d m b n e d a o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
the value of the median: a //对o的左边部分经行快速排序
during:>a a a a n b m e f c g d l h c b h l b c e d g c f e d m b n e d b o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
after:>a a a a n b m e f c g d l h c b h l b c e d g c f e d m b n e d b o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
the value of the median: b
during:>a a a a b b b b f c g d l h c e h l m c e d g c f e d m n n e d b o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
after:>a a a a b b b b b c g d l h c e h l m c e d g c f e d m n n e d f o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
the value of the median: d
during:>a a a a b b b b b d d d c c c c h l m e e h g l f e f m n n e g d o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
after:>a a a a b b b b b c c c c d d d d l m e e h g l f e f m n n e g h o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
the value of the median: h
during:>a a a a b b b b b c c c c d d d d h g e e e g f f e l m n n l m h o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
after:>a a a a b b b b b c c c c d d d d e g e e e g f f h h m n n l m l o o o x v w w y r x r r u x q p z v t z p t v z q u x u r y r x r w w v x z
the value of the median: x //对o的右边部分经行快速排序
during:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o x x x w v r v r r u w q p w v t r p t v w q u r u r y z z z z y x x x
after:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o r u r w v r v r r u w q p w v t r p t v w q u x x x x x x z z y z z y
the value of the median: r
during:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o r r r r p q p q v u w u v w v t w u t v w r r x x x x x x z z y z z y
after:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o q p q p r r r r r r w u v w v t w u t v w u v x x x x x x z z y z z y
the value of the median: w
during:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o p p q q r r r r r r w w v v v t u u t v u w w x x x x x x z z y z z y
after:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o p p q q r r r r r r u v v v v t u u t w w w w x x x x x x z z y z z y
the value of the median: u
during:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o p p q q r r r r r r u u u t t v v v v w w w w x x x x x x z z y z z y
after:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o p p q q r r r r r r t t u u u v v v v w w w w x x x x x x z z y z z y
finish:>a a a a b b b b b c c c c d d d d e e e e f f g g h h l l m m n n o o o p p q q r r r r r r t t u u u v v v v w w w w x x x x x x y y z z z z
原文:http://www.cnblogs.com/kirov/p/5041075.html