[有向图强连通分量]
有向图强连通分量的Tarjan算法
在有向图G中,如果两个顶点间至少存在一条路径,称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。非强连通图有向图的极大强连通子图,称为强连通分量(strongly connected components)。
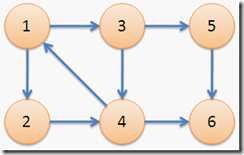
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
[Tarjan算法]
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
[演示]
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
算法结束。求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
可以发现,运行Tarjan算法的过程中,每个顶点都被访问了一次,且只进出了一次堆栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(N+M)。
[模板]
1 /*==================================================*\ 2 | Tarjan强连通分量 3 | INIT: vec[]为邻接表; stop, cnt, scnt置0; id[],pre[]置-1; 4 | CALL: for(i=0; i<n; ++i) if(-1==pre[i]) tarjan(i, n); 5 | 6 | vec[] :邻接表 7 | id[] :属于哪个分量,对应范围:0~cnt-1 8 | pre[m]:记录m的是第几次访问,同时如果pre[m]==-1则表明m未访问 9 | vec[] :为邻接表 10 | s[] :栈 11 | stop :栈顶指针 12 | scnt :强连通分量的个数 13 | cnt :访问计数 14 | void tarjan(int v, int n) :v为当前访问节点 15 \*==================================================*/ 16 vector<int> vec[V]; int id[V], pre[V], low[V], s[V], stop, cnt, scnt; 17 void tarjan(int v) 18 { 19 int t, minc = low[v] = pre[v] = cnt++; //初始均赋值为当前节点 20 vector<int>::iterator pv; 21 s[stop++] = v; //当前节点入栈 22 for (pv = vec[v].begin(); pv != vec[v].end(); ++pv) 23 { 24 if(-1 == pre[*pv]) //如果未访问过 25 tarjan(*pv); 26 if(low[*pv] < minc) //更新最小节点 27 minc=low[*pv]; 28 } 29 if(minc < low[v]) //找到环路,更新low[v],并返回; 30 { 31 low[v] = minc; 32 return; 33 } 34 do //弹出该分量 35 { 36 id[t = s[--stop]] = scnt; //出栈 37 low[t] = low[v]; 38 } while(t != v); 39 ++scnt; // 强连通分量的个数 40 }
[例子]
题目:高速公路
#include<iostream> #include<queue> #include<cmath> #include<cstring> #include<vector> #include<set> using namespace std; #define V 10005 int m,n; vector<int> vec[V]; int id[V], pre[V], low[V], s[V], stop, cnt, scnt; void tarjan(int v) { int t, minc = low[v] = pre[v] = cnt++; //初始均赋值为当前节点 vector<int>::iterator pv; s[stop++] = v; //当前节点入栈 for (pv = vec[v].begin(); pv != vec[v].end(); ++pv) { if(-1 == pre[*pv]) //如果未访问过 tarjan(*pv); if(low[*pv] < minc) //更新最小节点 minc=low[*pv]; } if(minc < low[v]) //找到环路,更新low[v],并返回; { low[v] = minc; return; } do //弹出该分量 { id[t = s[--stop]] = scnt; //出栈 low[t] = low[v]; } while(t != v); ++scnt; // 强连通分量的个数 } int main() { //初始化 freopen("in.txt","r",stdin); cin>>m>>n; int a,b; for (int i = 1; i <= n; i++) { cin>>a>>b; vec[a].push_back(b); } memset(pre,-1,sizeof(pre)); memset(id,-1,sizeof(id)); //求解 for (int i = 1; i <= m; i++) { if(pre[i]==-1)//访问所有未标记的点 tarjan(i); } int id_count[V]; memset(id_count,0,sizeof(id_count)); //记录每个分量组元素个数 for (int i = 1; i <= m; i++) { id_count[id[i]]++; } //求解 int acount=0; for (int i = 0; i < scnt; i++) { acount+=(id_count[i]-1)*id_count[i]/2; } cout<<acount; return 0; }
原文:http://www.cnblogs.com/whzlw/p/5042023.html