大数问题是指操作数超过了计算机常用数据类型的存储范围,常常是用字符串来模仿整数相加和相乘运算来实现的,在模拟的过程中要注意考虑进位和边界条件。
1、大整数相加
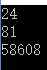
先看一下加法的计算过程,如456+56789
456
56789
---------
57245
计算过程是从低位往高位开始计算,计算过程要加上进位,如,计算到5+8的时候要加上前面的进位1,得到14,然后14对10取余作为对应结果的第2位,进位为14对10取正,这样一直计算,直到有一个字符串结束,然后考虑进位和没计算完的另一个字符串相加。
边界条件:
两个大整数相加,结果的长度可能与两个数中长度较大的一个相等,也可能比其大1(进位造成),如123+12=135,123长度为3,12长度为2,结果长度为3,再如99+1=100,结果长度为3比99的长度还大1。
考虑到这样的边界条件,在申请内存的时候需要对结果至少申请长度较大的那个还要大1。
代码如下:
#include<iostream> #include<string> using namespace std; //字符串倒置 void reverse(char *str) { int len=strlen(str); for(int i=0;i<len/2;i++) { char temp=str[i]; str[i]=str[len-i-1]; str[len-i-1]=temp; } } //大数求和 void bignumsum(char * ope1,char * ope2,char * result) { reverse(ope1); reverse(ope2); int len1=strlen(ope1); int len2=strlen(ope2); int max=len1; if(max<len2) { max=len2; } memset(result,‘0‘,max+1); result[max+1]=‘\0‘; int acc=0; int i=0; while(i<len1 && i<len2) { int temp=ope1[i]-‘0‘+ope2[i]-‘0‘+acc; acc=temp/10; result[i]=temp%10+‘0‘; i++; } if(i<len1) { while(i<len1) { int temp=ope1[i]-‘0‘+acc; acc=temp/10; result[i]=temp%10+‘0‘; i++; } } if(i<len2) { while(i<len2) { int temp=ope2[i]-‘0‘+acc; acc=temp/10; result[i]=temp%10+‘0‘; i++; } } //考虑到进位,所以result的长度有可能比ope1和ope2中最大的数据长度还多出一位 if(acc) { result[i]=acc+‘0‘; } else { result[i]=‘\0‘; } reverse(result); } int main() { char num1[4]="456"; char num2[5]="5678"; char num3[6]; bignumsum(num1,num2,num3); cout<<num3<<endl; char num4[4]="456"; char num5[5]="678"; char num6[6]; bignumsum(num4,num5,num6); cout<<num6<<endl; char num7[4]="111"; char num8[5]="2"; char num9[6]; bignumsum(num7,num8,num9); cout<<num9<<endl; return 0; }

2、大整数相乘
乘法相对于加法稍微复杂一点,需要同时考虑乘法进位和加法进位,还要注意一下计算过程和结果中的对应关系。
如计算123*45
123
45
------
615
492
-------
5535
计算过程是从低位往高位计算,第2个操作数中每一位都与第一个操作数中的所有的位计算一次,而每这样计算一次都进行一次结果的更新,结果先被初始化成全0。而计算过程和结果的规律是,每次计算的时候影响的结果位数是两个操作数位数的和,如上述例子中1是123中的第2位(从低位算起,个位按0位来算),4是45中的第1位,那么这两个数的计算过程将会产生影响的是结果中的第3位,计算过程是1*4+0(上一次乘法的进位)=4,4%10=4,这样就确定了492位置上的那个4,然后再利用加法进位和上一轮的结果来更新结果,结果为0(原来结果对应该位的值)+4(此轮乘法计算之后该位置上对应的值)+1(上一轮加法的进位值)=5
边界条件:
两个大整数相乘结果的长度最大为两个操作数长度之和,所以申请内存的时候要注意至少申请两个操作数长度之和的内存。
代码如下:
#include<iostream> #include<string> using namespace std; void reverse(char *str) { int len=strlen(str); for(int i=0;i<len/2;i++) { char temp=str[i]; str[i]=str[len-i-1]; str[len-i-1]=temp; } } void bignummultiply(char *ope1,char *ope2,char *result) { reverse(ope1); reverse(ope2); int len1=strlen(ope1); int len2=strlen(ope2); memset(result,‘0‘,len1+len2);//因为len1和len2两个长度的整数相乘结果最大为len1+len2 result[len1+len2]=‘\0‘; int acc=0;//加法进位 int mcc=0;//乘法进位 for(int i=0;i<len2;i++) { acc=0; mcc=0; for(int j=0;j<len1;j++) { int temp1=(ope1[j]-‘0‘)*(ope2[i]-‘0‘)+mcc; mcc=temp1/10; temp1=temp1%10; int temp2=result[i+j]-‘0‘+temp1+acc; acc=temp2/10; result[i+j]=temp2%10+‘0‘; } result[i+len1]=acc+mcc+‘0‘; } //这里有一个去除后面0的程序,如78900\0将变成789\0,这样倒过来之后就会使987,而不是00987 int k=len1+len2-1; while(‘0‘==result[k] && k>=0) { result[k--]=‘\0‘; } //最后经result倒置回来得到最终结果 reverse(result); } int main() { char n1[5]="12"; char n2[5]="2"; char n3[10]; bignummultiply(n1,n2,n3); cout<<n3<<endl; char n4[5]="9"; char n5[5]="9"; char n6[10]; bignummultiply(n4,n5,n6); cout<<n6<<endl; char n7[5]="888"; char n8[5]="66"; char n9[10]; bignummultiply(n7,n8,n9); cout<<n9<<endl; return 0; }
以上加法和乘法的计算过程都先使用reverse将字符串倒置,然后再将结果倒置回来计算的,这样是为了更直观的计算,但是,这样会使程序运行效率稍低。实际可以不用倒置,而靠逻辑去写。
原文:http://www.cnblogs.com/bewolf/p/5055485.html