1.贝叶斯定理 设X是数据元组。在贝叶斯的术语中,X看做是证据。通常,X用n个属性集的测量值描述。令H为某种假设,如数据元组X属于某个特定类C。对于分类问题,希望确定给定证据或者观测数据元组X,假设H成立的概率为P(H|X)。换言之,给定X的属性描述,找出元组X属于类C的概率。
P(H|X)是后验概率,或在条件X下,H的后验概率。例如,设数据元组限于分别由属性age和income描述的顾客,而X是一位35岁的顾客,其年收入为4万美元。令H为某种假设,如顾客将购买计算机。则P(H|X)反映当我们知道顾客年龄和收入时,顾客X将购买计算机的概率。
相反,P(H)是先验概率,或H的先验概率。对于我们的例子,它是任意给定顾客将购买计算机的概率,而不管他们的年龄,收入或任何其他的信息。后验概率P(H|X)比先验概率P(H)基于更多的信息(例如顾客的信息)。P(H)独立于X。
类似地,P(X|H)是条件H下,X的后验概率。也就是说,它是已知顾客X将要购买计算机,该顾客的年龄为35岁并且收入时4万美元的概率。
P(X)是X的先验概率。它是顾客集合中的年龄为35岁并且收入为4万美元的概率。
如何估计这些概率?正如下面将要看到的,P(X),P(H),和P(X|H)可以由给定的数据进行估计。贝叶斯定理是有用的,它提供了一种由P(X)、P(H)、P(X|H)计算后验概率P(H|X)的方法。贝叶斯定理如下:
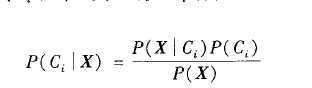 公式1
公式1
朴素贝叶斯分类法或者简单贝叶斯分类法的工作过程如下:
(1)设D是训练元组和他们相关联的类标号的集合。通常,每个元组用一个n维属性向量X={X1,X2,....Xn}表示,描述由n个属性A1,A2,...An对元组的n个测量。
(2)假定有m个类C1,C2,...Cm。给定元组X,分类法将预测X属于具有最高后验概率的类(在条件X下)。也就是说,朴素贝叶斯分类法预测X属于类Ci,当且仅当P(Ci|X)>P(Cj|X) j∈[1,m] j≠i。这样,最大化P(Ci|X)。P(Ci|X)最大的类Ci称为最大后验概率。根据贝叶斯定理,
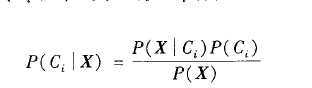 公式1
公式1
(3)由于P(X)对所有类为常数,所以只需要P(X|Ci)P(Ci)最大即可。如果类的先验概率未知,则通常假设这些类是等概率的,即P(C1)=P(C2)=...=P(Cn),并且据此对P(X|Ci)最大化,否则,最大化P(X|Ci)P(Ci)。注意,类先验概率可以用P(Ci)=|C i,D|/|D|估计,其中|Ci,D|是D中Ci类的训练元组数目。
(4)给定具有许多属性的数据集,计算P(X|Ci)的开销可能非常大。为了降低计算P(X|Ci)的开销,可以做类条件独立的朴素假定。给定元组的类标号,假定属性值有条件地相互独立(即属性之间不存在依赖关系)。因此有:
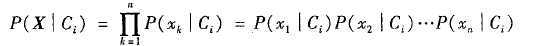 公式2
公式2
可以很容易地由训练元组估计概率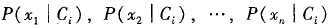 。注意,Xk表示元组X在属性Ak的值。对于每个属性,考察该属性是分类的还是连续值的。例如,为了计算
。注意,Xk表示元组X在属性Ak的值。对于每个属性,考察该属性是分类的还是连续值的。例如,为了计算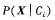 ,考虑以下的情况:
,考虑以下的情况:
(1)如果Ak是分类属性,则P(Xk|Ci)是D中属性Ak值为Xk的Ci类的元组数目除以D中Ci类的元组数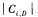 。
。
(2)如果Ak是连续值属性,则需要多做一点工作,但是计算很简单。通常,假定连续值属性服从均值为μ,标准差为σ的高斯分布,由下式定义:
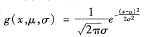 公式3
公式3
因此:
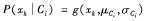 公式4
公式4
这些公式看上去可能有点令人生畏,但是沉住气!需要计算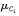 和
和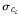 ,它们分别是Ci类训练元组属性Ak的均值和标准差。将这两个量与Xk一起带入公式3,计算P(Xk|Ci)。
,它们分别是Ci类训练元组属性Ak的均值和标准差。将这两个量与Xk一起带入公式3,计算P(Xk|Ci)。
例如,设X=(35,40000美元),其中A1和A2分别是属性age和income。设类标号属性为buys_computer。X相关联的类标号是“yes”。假设age尚未离散化,因此是连续值属性。假设从训练集之中发现D中购买计算机的顾客年龄为38 ±12岁。换言之,对于属性age和这个类,有μ=28,σ=12。可以把这些量与元组X的x1=35一起带入公式3,估计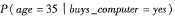 。
。 2.贝叶斯分类法的效果:
该分类法与决策树和神经网络分类法的各种比较试验表明,在某些领域,贝叶斯分类法足以和它们相媲美。理论上讲,与其他所有分类算法相比,贝叶斯分类法具有最小的错误率。然而实践之中并非一直如此。这是由于对其使用的假定类条件独立性的不确定性,以及缺乏可用的概率数据造成的。
贝叶斯分类还可以用来为不直接使用贝叶斯定理的其他分类法提供理论判定。例如,在某种假定下,可以证明,与朴素贝叶斯分类法一样,许多神经网络和曲线拟合算法输出最大的后验假定。
3.一个例子:
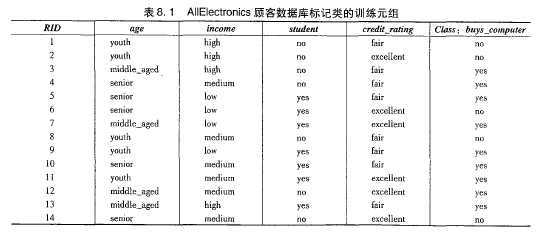
数据元组用属性age、income、student、和credit_rating描述。类标号属性buys_computer具有两个不同值,yes和no。希望分类的元组是X=(age=youth,income=medium,student=yes,credit_rating=fair),需要最大化P(X|Ci)P(Ci),i=1,2。没各类的先验概率P(Ci)可以根据训练元组计算:
P(buys_computer=yes)=9/14=0.643
P(buy_computer=no)=5/14=0.357
为了计算P(X|Ci),i=1,2,计算下面的条件概率:
P(age=youth|buys_computer=yes) =2/9=0.222
P(age=youth|buys_computer=no) =3/5=0.600
P(income=medium|buys_computer=yes) =4/9=0.444
P(income=medium|buys_computer=no) =2/5=0.400
P(student=yes|buy_computer=yes) =6/9=0.667
P(student=no|buy_computer=yes) =1/5=0.200
P(credit_rating=fair|buy_computer=yes) =6/9=0.667
P(credit_rating=fair|buy_computer=no) =2/5=0.400
所以就有P(X|buys_computer=yes) = P(age=youth|buys_computer=yes)*
P(income=medium|buys_computer=yes)*
P(student=yes|buy_computer=yes)*
P(credit_rating=fair|buy_computer=yes)
= 0.222*0.444*0.667*0.667=0.044
也有:
P(X|buys_computer=no) = P(age=youth|buys_computer=no)*
P(income=medium|buys_computer=no)*
P(student=yes|buy_computer=no)*
P(credit_rating=fair|buy_computer=no)
= 0.600*0.400*0.200*0.400=0.019
为了找到最大化的P(X|Ci)P(Ci)的类,计算:
P(X|buys_computer=yes)P(buys_computer=yes)=0.044*9/14=0.028
P(X|buys_computer=no)P(buys_computer=no)=0.019*5/14=0.007
所以,对于元组X,朴素贝叶斯分类预测元组X的类别为buys_computer=yes。
4.对于0概率的特殊处理
如果得到某个p(Xk|Ci)的零概率值,那么P(X|Ci)=0,现在还怎么继续玩下去?
有一个简单的技巧来避免此问题。可以假定训练的数据库D很大,以至于每个计数加1造成的估计概率的变化可以忽略不计。如果对q个计数都加上1,则必须记住在用于计算概率的对应分母上加上q。这种概率估计计数称为拉普拉斯校准或者拉普拉斯估计法。
附例:
假设在某个训练数据库D上,类buys_computer=yes包含由1000个元组,有0个元组income=low,990个元组income=medium,10个元组income=high。不使用拉普拉斯校准,这些事情的概率分别是0,0.990,0.010。对这三个量使用拉普拉斯校准,假定对每个收入--值对增加一各元组。用这种方法,分别得到如下的概率:
1/1003 =0.001 991/1003=0.988 11/1003=0.011
这些校准的概率和对应的未校准的估计很接近,但是避免了0概率值。
朴素贝叶斯算法原理
原文:http://www.cnblogs.com/zhoudayang/p/5058264.html
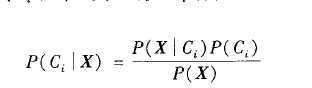 公式1
公式1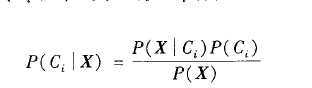 公式1
公式1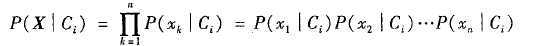 公式2
公式2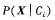 ,考虑以下的情况:
,考虑以下的情况: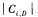 。
。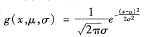 公式3
公式3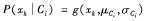 公式4
公式4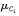 和
和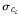 ,它们分别是Ci类训练元组属性Ak的均值和标准差。将这两个量与Xk一起带入公式3,计算P(Xk|Ci)。
,它们分别是Ci类训练元组属性Ak的均值和标准差。将这两个量与Xk一起带入公式3,计算P(Xk|Ci)。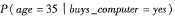 。
。